Problems

Pascal’s triangle, (known as Khayyam’s triangle in Iran and Yang Hui’s triangle in China) is seen below.

Well, what does it mean? We start with diagonal lines of 1s. Then every other number in the interior is the sum of the two numbers above it. With this simple rule, the triangle shows lots of cool structure.

Today we’ll look at various problems involving probability. [do we need more of an introduction?]

Today we’ll look at 3-dimensional shapes, including their volumes and surfaces areas. One special kind are the Platonic Solids - the tetrahedron, cube, octahedron, dodecahedron and icosahedron.

Today we’ll look at various logic puzzles where you have to imagine what’s going on inside someone else’s head. What they’re thinking about could be about what’s going on inside your own head!

We’ll look at ways of making big numbers today. Hopefully you know about powers of numbers. Most of the biggest numbers you’ve seen probably involve powers. Powers are typically thought of as ’repeated multiplication’. You could think of this as being similar to how multiplication is ’repeated multiplication’.

We might use powers when decimal representation is far too long to be useful for understanding the size of an object.

But what if powers aren’t helpful enough? Mathematician and computer scientist Donald Knuth introduced Knuth’s up-arrow notation. A single up-arrow means ‘raise to the power of’. So \(2\uparrow5=2^5=2\times2\times2\times2\times2=32\). Recall that the \(5\) means we have five \(2\)s. Two arrows means ‘tetration’. For example \(2\uparrow\uparrow4=2\uparrow(2\uparrow(2\uparrow2))=2^{(2^{(2^2)})}=2^{(2^4)}=2^{16}=65536\). The \(4\) means that we have four \(2\)s. Three arrows means pentation. So \(2\uparrow\uparrow\uparrow3=2\uparrow\uparrow(2\uparrow\uparrow2)\). Here the \(3\) means that there are three \(2\)s. Remember that \(2\uparrow\uparrow2=2\uparrow2=2^2=4\). So \(2\uparrow\uparrow\uparrow3=2\uparrow\uparrow4=65536\).

A million is \(10^6\) and a billion is \(10^9\). A million seconds is about eleven and a half days. A billion seconds is about 31 years. Other famous big numbers are googol, Skewes’ number, Graham’s number, busy beaver and TREE(3). Another classic big number is the number of atoms in the observable universe - about \(10^{80}\). This is less than \(4\uparrow\uparrow3\), \(3\uparrow\uparrow\uparrow3\), or \(2\uparrow\uparrow\uparrow\uparrow3\).

A couple of these problems are Fermi problems, named after physicist Enrico Fermi. This is where you try to estimate a quantity in the real world. We’re not expecting an exact answer (indeed, we don’t know the exact answer), but using some intelligent estimation, you can get a good idea of the answer.

We bet that some of you play chess and are pretty good. Someone may be better than all of the tutors. Unfortunately for that person, and fortunately for the rest of you, that won’t help too much with the problems today. You’ll need to know how the pieces move and that’s it.

There are various themes of knight’s tours, independence and queens’ domination. We also won’t just look at typical \(8\times8\) chessboards, but grids of different sizes, and even ones that aren’t flat.

You may have seen the first example (seen below) previously. Before we get to that, let’s introduce some notation. We write \(K_n\) for the complete graph on \(n\) vertices - that is, every possible edge is present.

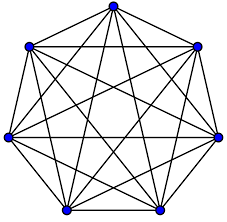
Note that edges don’t have a direction, and are between pairs of different vertices. Ramsey theory looks at what happens when we colour every edge in \(K_n\) either red or blue. Are we guaranteed a red \(K_3\) subgraph? No, because we could just colour every edge in \(K_n\) blue. Instead, we ask if we are guaranteed a red \(K_3\) or a blue \(K_3\) subgraph? It turns out yes, so long as \(n\) is big enough.

We can then look at extensions to this problem. We write \(R(s,t)\) for the least number \(n\) such that whenever you colour the edges of \(K_n\) in red or blue, then you’re guaranteed a red \(K_s\) or a blue \(K_t\). By least \(n\), this means that there’s a colouring of the edges of \(K_{n-1}\) with no red \(K_s\) or blue \(K_t\).

You may like to use the inequality \(R(m,n)\le R(m,n-1)+R(m-1,n)\). Furthermore, when both \(R(m,n-1)\) and \(R(m-1,n)\) are even, we have the stronger inequality of \(R(m,n)\le R(m,n-1)+R(m-1,n)-1\).