Problems
Tile a \(5\times6\) rectangle in an irreducible way by laying \(1\times2\) rectangles.
Does there exist an irreducible tiling with \(1\times2\) rectangles of a \(4\times 6\) rectangle?
Irreducibly tile a floor with \(1\times2\) tiles in a room that is a \(5\times8\) rectangle.
Tile the whole plane with the following shapes:

David Smith cut out 12 nets. He claimed that it was possible to make a cube out of each net. Roger Penrose looked at the patterns, and after some considerable thought decided that he was able to make cubes from all the nets except one. Can you figure out which net cannot make a cube?

It is known that it is possible to cover the plane with any cube’s net. Show how you can cover the plane with this net:

After removing a \(1\times 1\) square from the corner of a \(4\times 4\) square, we are left with the following shape:

how can we cut this into three congruent shapes?
Can a \(5\times5\) square checkerboard be covered by \(1\times2\) dominoes?
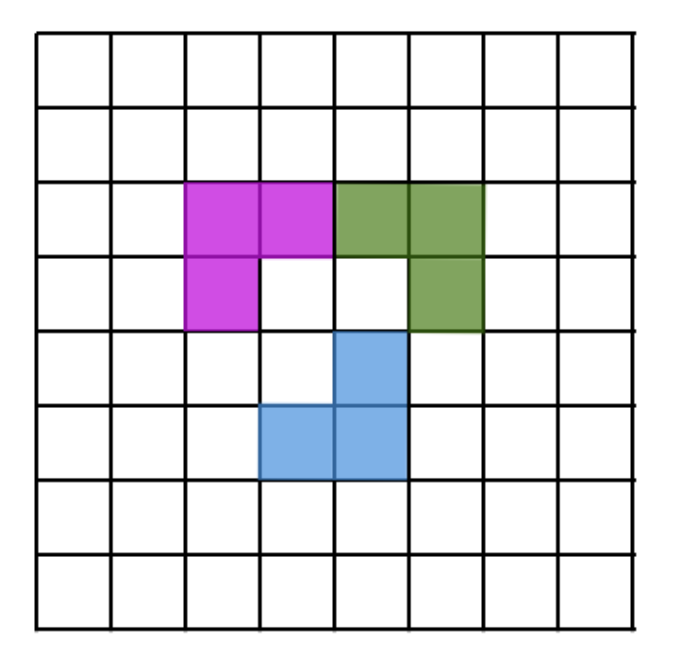
Can you cover a \(10 \times 10\) board using only \(T\)-shaped tetraminoes?
On an 8×8 grid (like a chessboard), an L-corner is a shape made of 3 little squares of the board that touch to make an L. You can turn the L any way you like. We place the L-corners so that none overlap. What is the fewest L-corners you must place so that no more L-corners can be added anywhere? Here is an example of how three L-corners may look like: