Problems

Tile a \(5\times6\) rectangle in an irreducible way by laying \(1\times2\) rectangles.

Does there exist an irreducible tiling with \(1\times2\) rectangles of a \(4\times 6\) rectangle?

Irreducibly tile a floor with \(1\times2\) tiles in a room that is a \(5\times8\) rectangle.

Tile the whole plane with the following shapes:

David Smith cut out 12 nets. He claimed that it was possible to make a cube out of each net. Roger Penrosae looked at the patterns, and after some considerable thought decided that he was able to make cubes from all the nets except one. Can you figure out which net cannot make a cube?

It is known that it is possible to cover the plane with any cube’s net. Show how you can cover the plane with nets below:

Remove a \(1 \times 1\) square from the corner of a \(4 \times 4\) square. Can this shape be dissected into \(3\) congruent parts?

Can a \(5\times5\) square checkerboard be covered by \(1\times2\) dominoes?

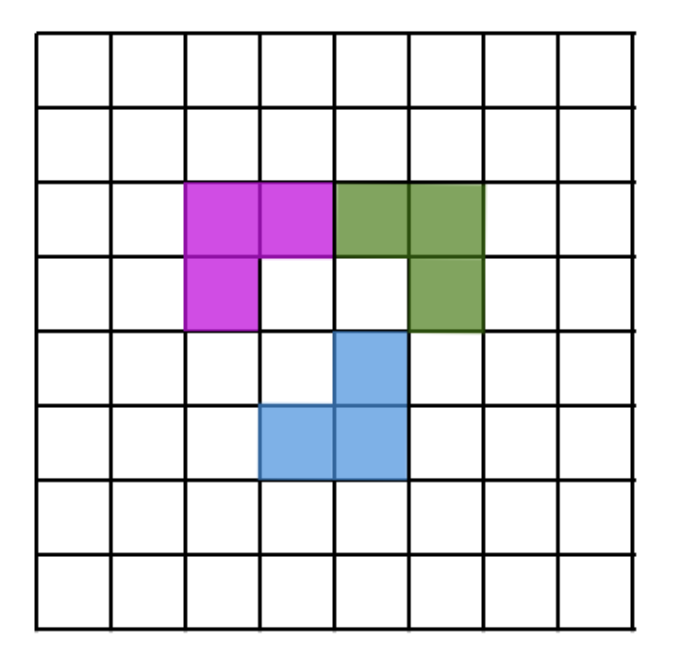
Can you cover a \(10 \times 10\) board using only \(T\)-shaped tetraminoes?

What is the smallest number of ‘L’ shaped ‘corners’ out of 3 squares that can be marked on an \(8\times 8\) square grid, so that no more ’corners’ would fit?