Out of the given numbers 1, 2, 3, ..., 1000, find the largest number \(m\) that has this property: no matter which \(m\) of these numbers you delete, among the remaining \(1000 - m\) numbers there are two, of which one is divisible by the other.
Author: A.A. Egorov
Calculate the square root of the number \(0.111 \dots 111\) (100 ones) to within a) 100; b) 101; c)* 200 decimal places.
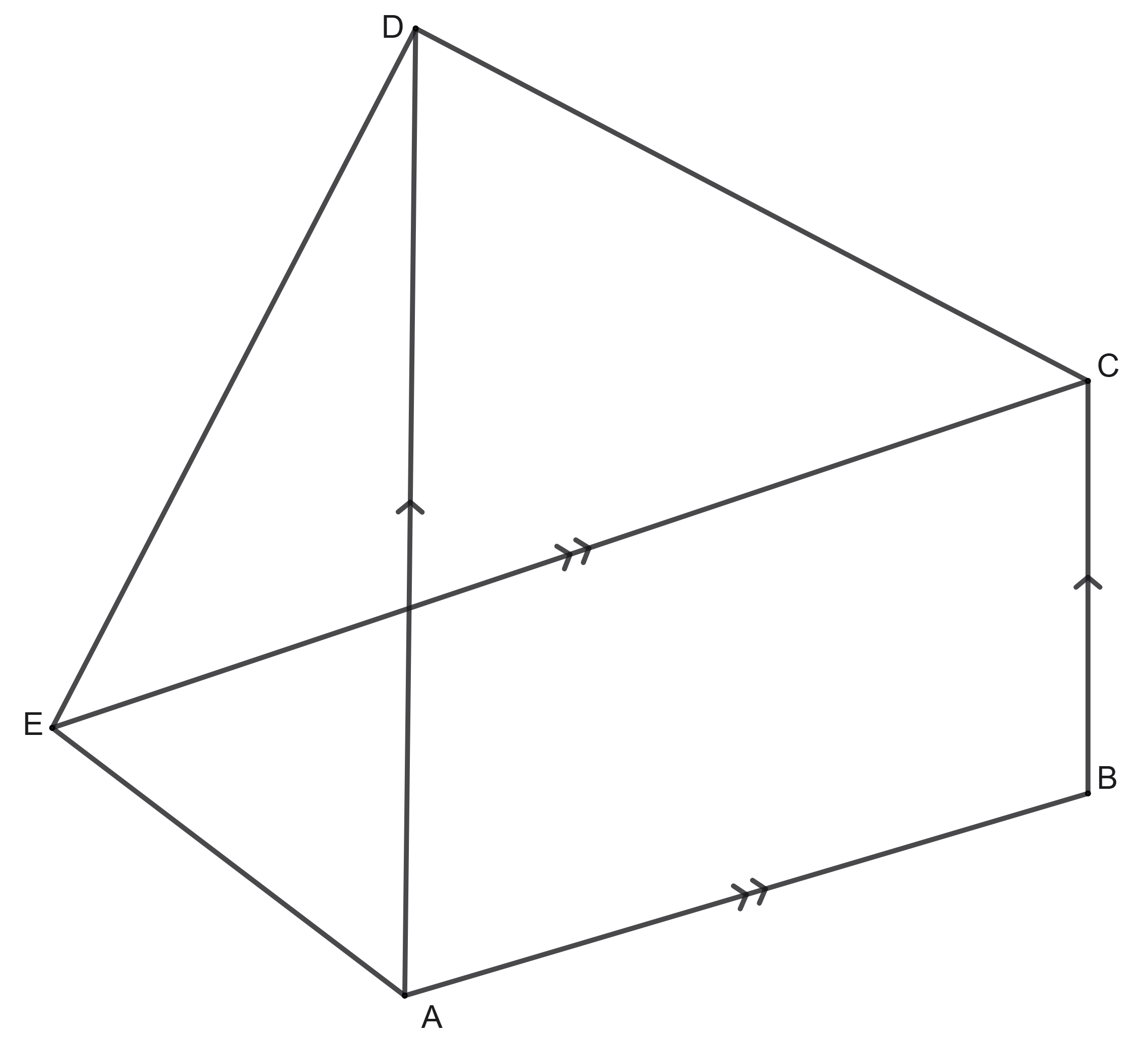
The triangle visible in the picture is equilateral. The hexagon inside is a regular hexagon. If the area of the whole big triangle is \(18\), find the area of the small blue triangle.
A quadrilateral is given; \(A\), \(B\), \(C\), \(D\) are the successive midpoints of its sides, \(P\) and \(Q\) are the midpoints of its diagonals. Prove that the triangle \(BCP\) is equal to the triangle \(ADQ\).
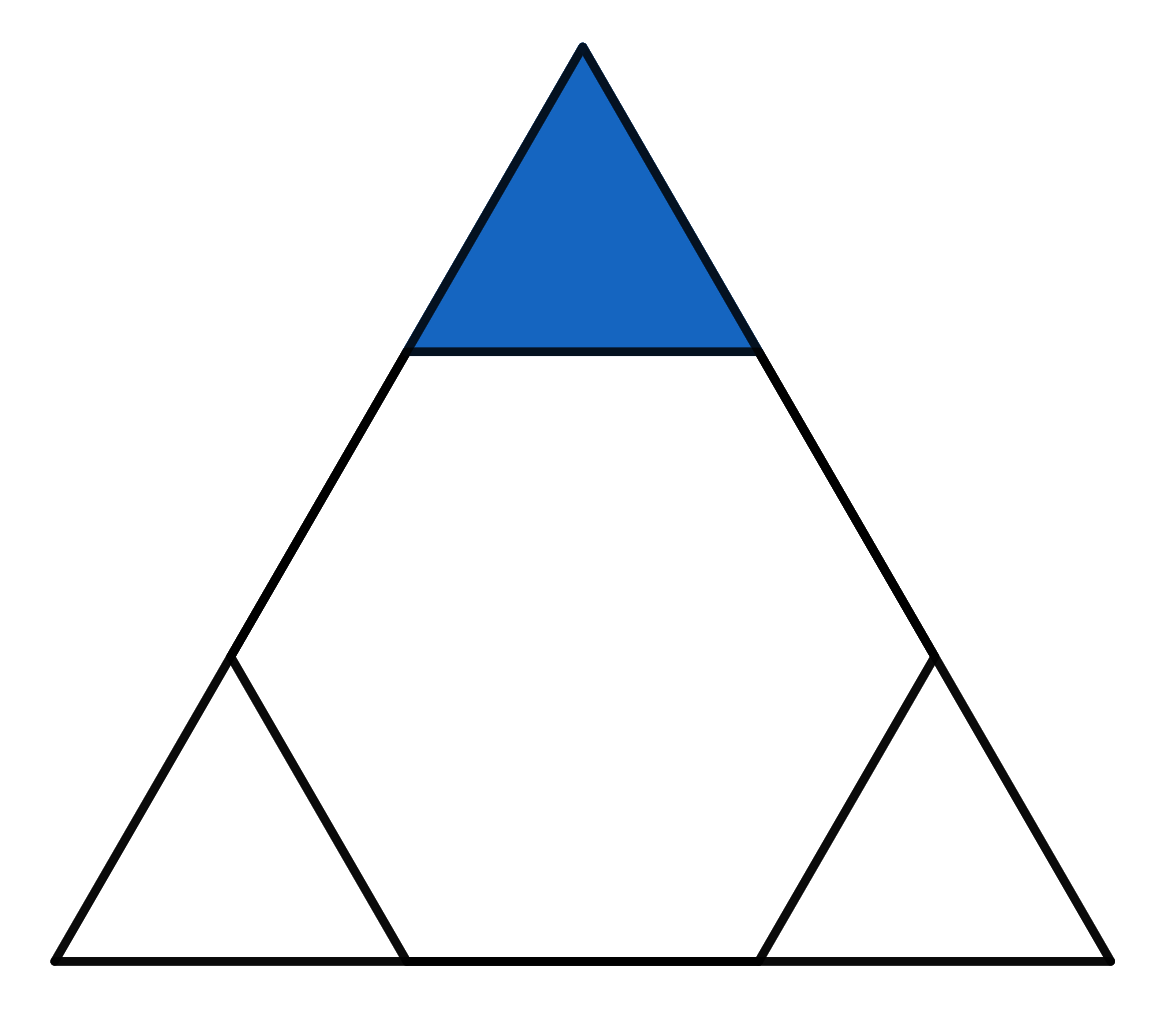
On the left there is a circle inscribed in a square of side 1. On the right there are 16 smaller, identical circles, which all together fit inside a square of side 1. Which area is greater, the yellow or the blue one?
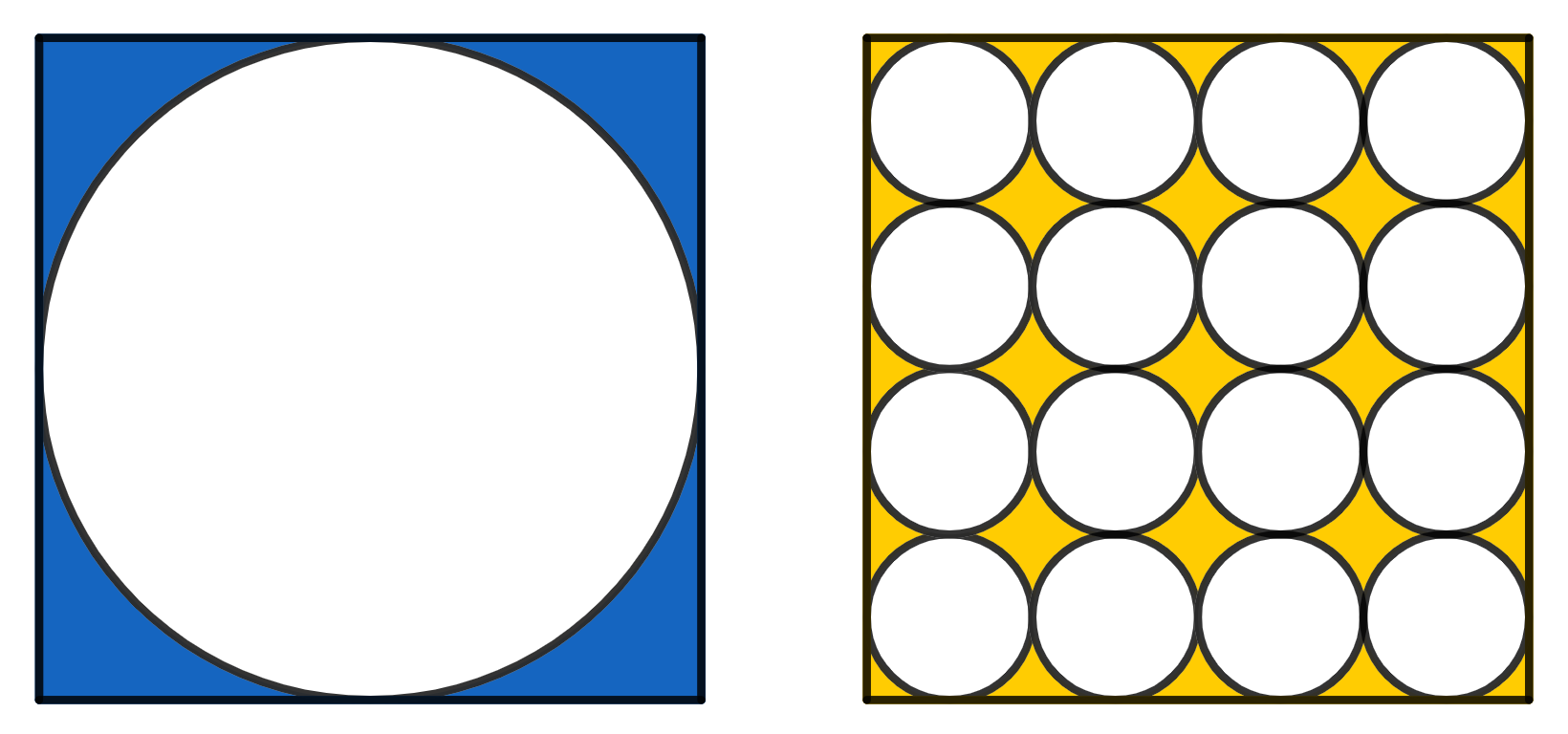
In a pentagon \(ABCDE\), diagonal \(AD\) is parallel to the side \(BC\) and the diagonal \(CE\) is parallel to the side \(AB\). Show that the areas of the triangles \(\triangle ABE\) and \(\triangle BCD\) are the same.
120 unit squares are placed inside a \(20 \times 25\) rectangle. Prove that it will always be possible to place a circle with diameter 1 inside the rectangle, without it overlapping with any of the unit squares.
You are given \(7\) straight lines on a plane, no two of which are parallel. Prove that there will be two lines such that the angle between them is less than \(26^{\circ}\).
Two lines on the plane intersect at an angle \(\alpha\). On one of them there is a flea. Every second it jumps from one line to the other (the point of intersection is considered to belong to both straight lines). It is known that the length of each of her jumps is 1 and that she never returns to the place where she was a second ago. After some time, the flea returned to its original point. Prove that for the angle \(\alpha\) the value \(\alpha/\pi\) is a rational number.
On a circle of radius 1, the point \(O\) is marked and from this point, to the right, a notch is marked using a compass of radius \(l\). From the obtained notch \(O_1\), a new notch is marked, in the same direction with the same radius and this is process is repeated 1968 times. After this, the circle is cut at all 1968 notches, and we get 1968 arcs. How many different lengths of arcs can this result in?