Problems
Cut an arbitrary triangle into parts that can be used to build a triangle that is symmetrical to the original triangle with respect to some straight line (the pieces cannot be inverted, they can only be rotated on the plane).
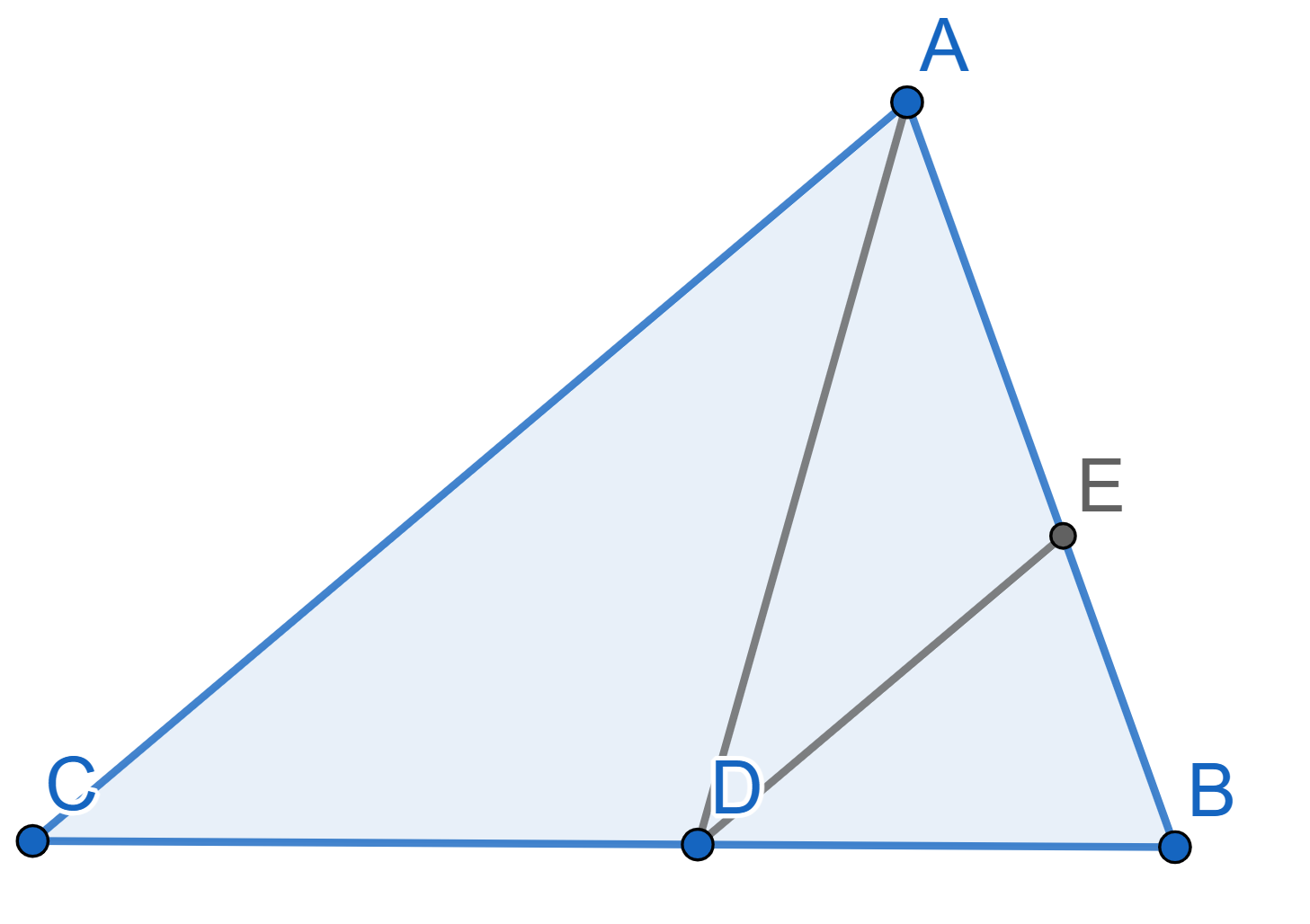
On the diagram below \(AD\) is the
bisector of the triangle \(ABC\). The
point \(E\) lies on the side \(AB\), with \(AE =
ED\). Prove that the lines \(AC\) and \(DE\) are parallel.
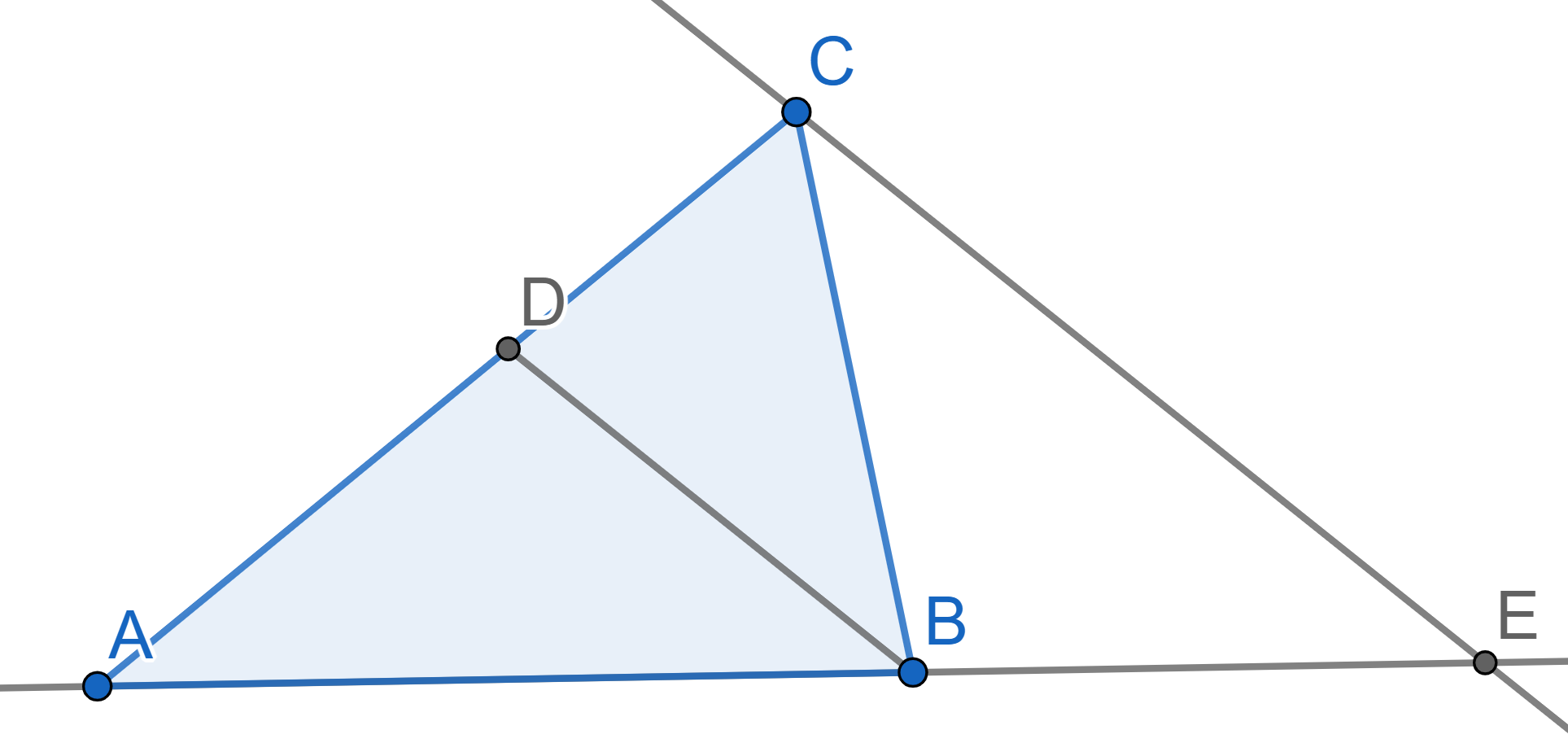
On the diagram below the line \(BD\)
is the bisector of the angle \(\angle
ABC\) in the triangle \(ABC\). A
line through the vertex \(C\) parallel
to the line \(BD\) intersects the
continuation of the side \(AB\) at the
point \(E\). Find the angles of the
triangle \(BCE\) triangle if \(\angle ABC = 110^{\circ}\).
It is easy to construct one equilateral triangle using three identical matches. Is it possible to construct four equilateral triangles by adding just three more matches identical to the original ones?
Look at the diagram below, which shows how to rearrange the pieces forming the first triangle.
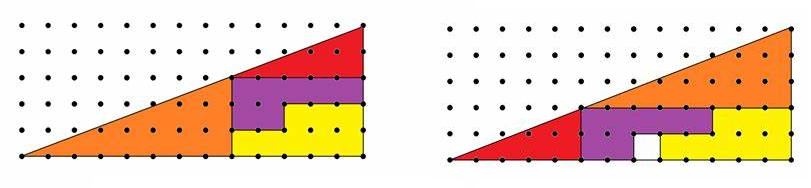
The shape seems unchanged, yet after looking more closely, we see that
the second picture appears to contain one extra square of area. How can
this be?
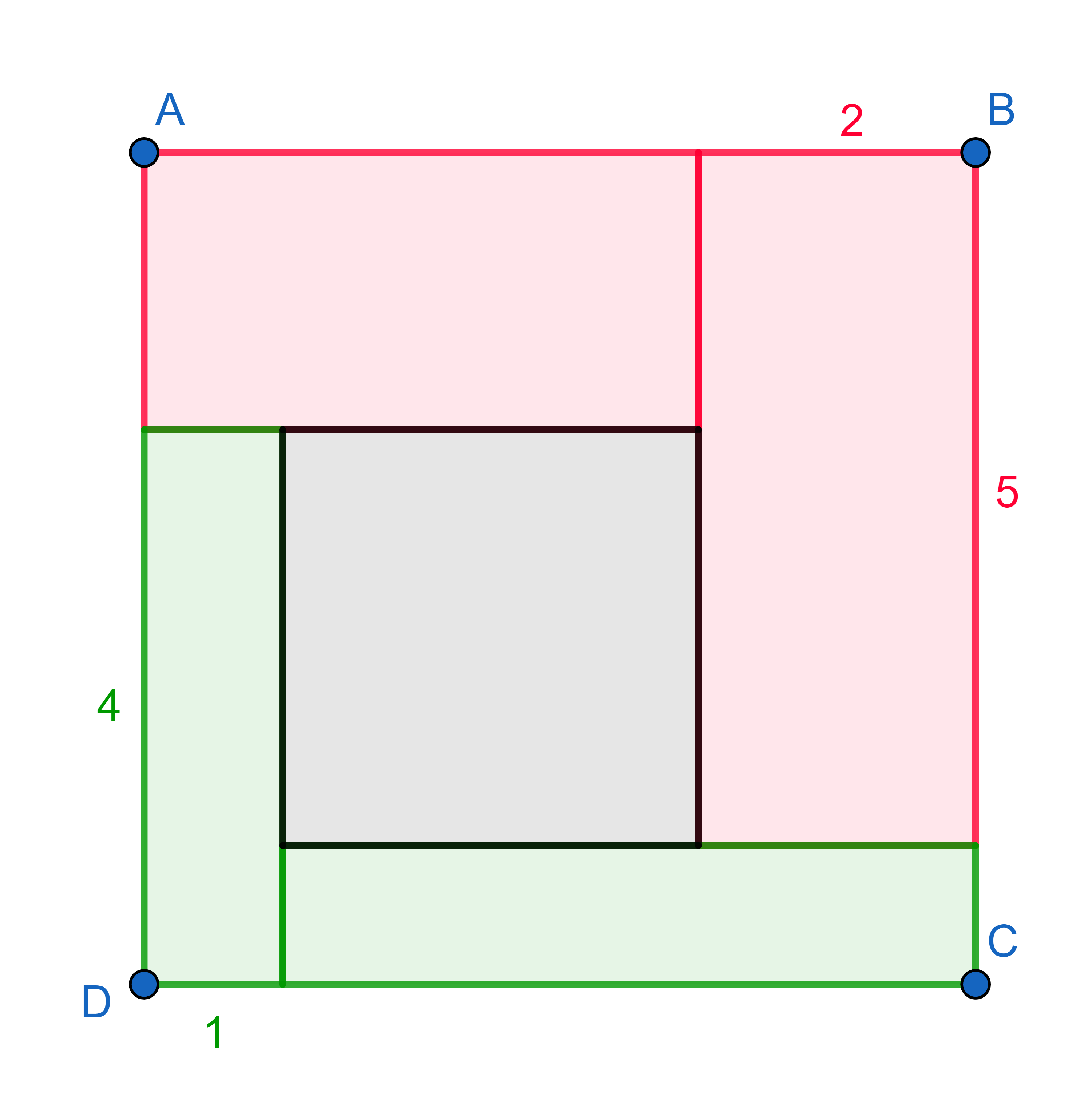
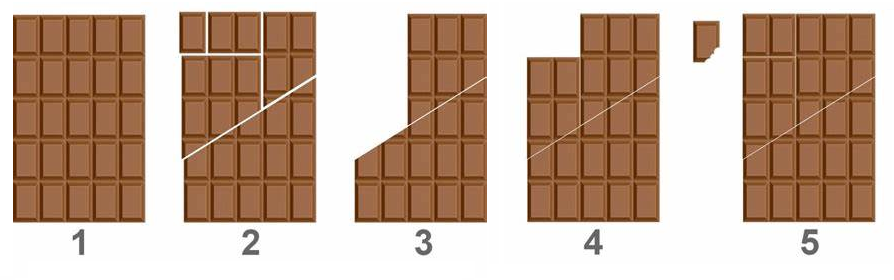
This problem is often called "The infinite chocolate bar". Depicted
below is a way to get one more piece of chocolate from the \(5\times 6\) chocolate bar. Do you see where
is it wrong?
Consider the following "proof" that any triangle is equilateral:
Given a triangle \(ABC\), we first
prove that \(AB = AC\). First let’s
draw the bisector of the angle \(\angle
A\). Now draw the perpendicular bisector of segment \(BC\), denote by \(D\) the middle of \(BC\) and by \(O\) the intersection of these lines. See
the diagram
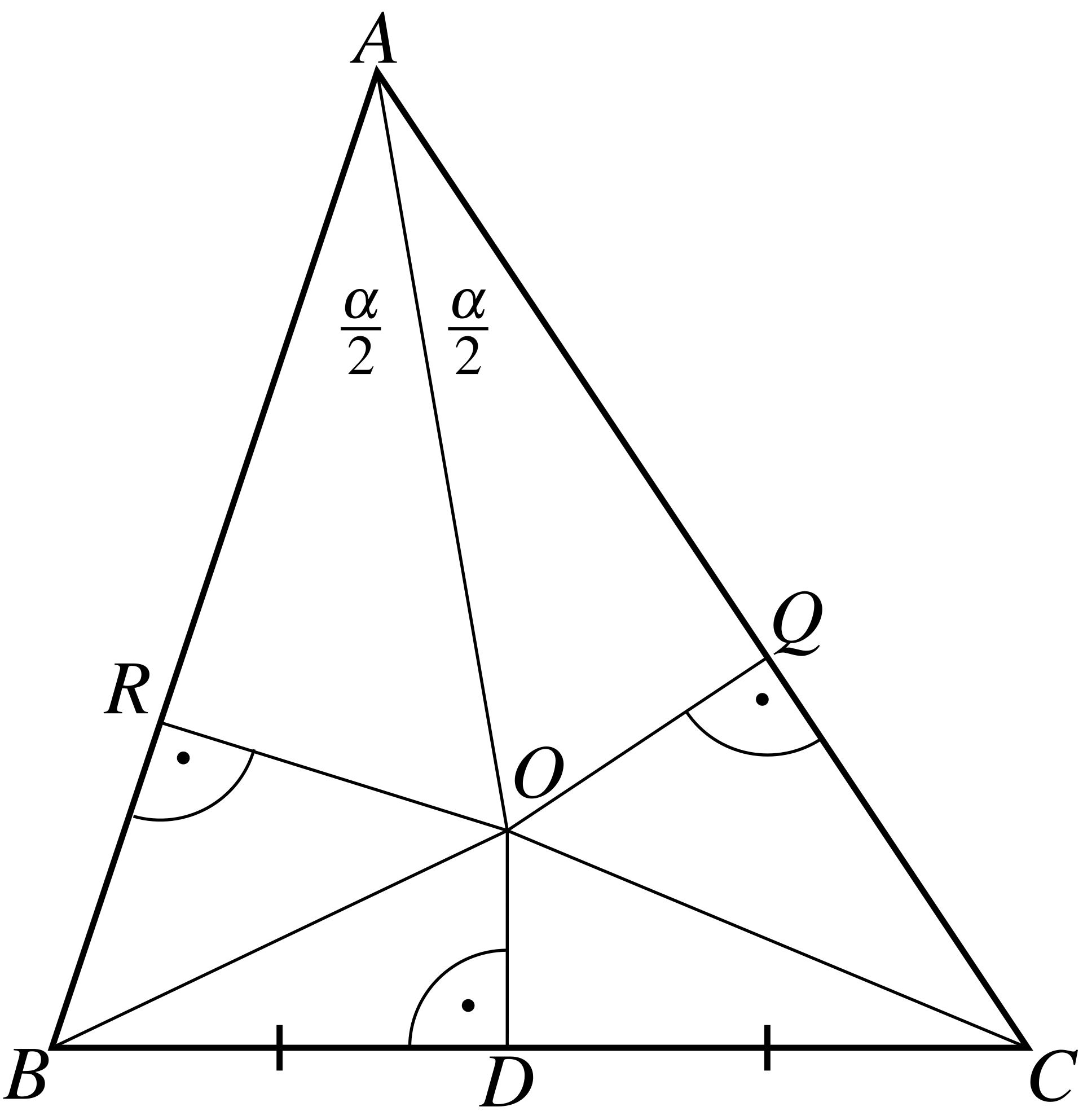
Draw the lines \(OR\) perpendicular to
\(AB\) and \(OQ\) perpendicular to \(AC\). Draw lines \(OB\) and \(OC\). Then the triangles, \(RAO\) and \(QAO\) are equal, since we have equal angles
\(\angle ORA = \angle OQA = 90°,\) and
\(\angle RAO = \angle QAO,\) and the
common side \(AO\). On the other hand
the triangles \(ROB\) and \(QOC\) are also equal since the angles \(\angle BRO = \angle CQO = 90°\), the
hypotenuses \(BO = OC\) the legs \(RO = OQ\). Thus, \(AR = AQ,\) \(RB =
QC,\) and \(AB = AR + RB = AQ + QC =
AC.\) Q.E.D.
As a corollary, one can show that all the triangles are equilateral, by showing that \(AB = BC\) in the same way.
Let’s prove that any \(90^{\circ}\)
angle is equal to any angle larger than \(90^{\circ}\). On the diagram
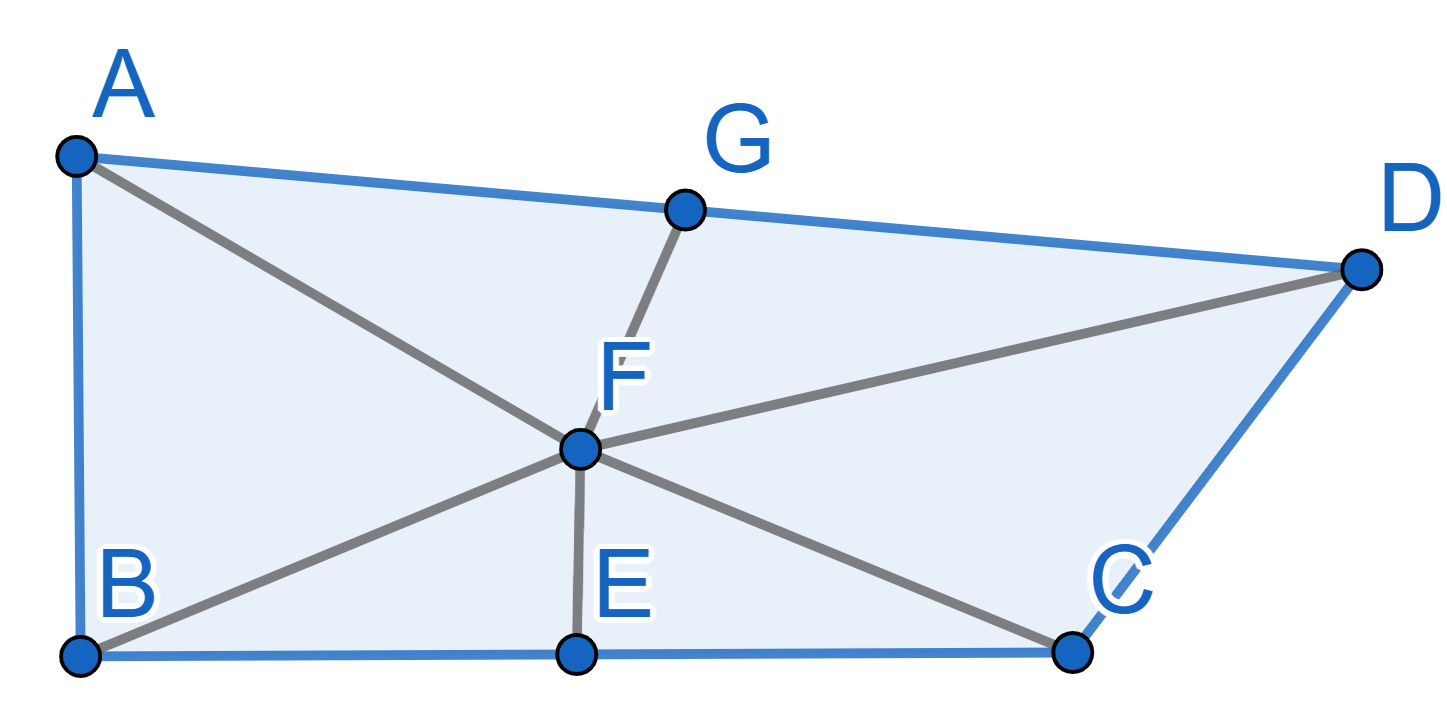
We have the angle \(\angle ABC =
90^{\circ}\) and angle \(\angle BCD>
90^{\circ}\). We can choose a point \(D\) in such a way that the segments \(AB\) and \(CD\) are equal. Now find middles \(E\) and \(G\) of the segments \(BC\) and \(AD\) respectively and draw lines \(EF\) and \(FG\) perpendicular to \(BC\) and \(AD\).
Since \(EF\) is the middle
perpendicular to \(BC\) the triangles
\(BEF\) and \(CEF\) are equal which implies the equality
of segments \(BF\) and \(CF\) and of angles \(\angle EBF = \angle ECF\), the same about
the segments \(AF=FD\). By condition we
have \(AB=CD\), thus the triangles
\(ABF\) and \(CDF\) are equal, thus \(\angle ABF = \angle DCF\). But then we have
\[\angle ABE = \angle ABF + \angle FBE =
\angle DCF + \angle FCE = \angle DCE.\]
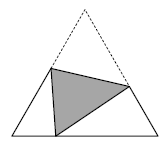
A equilateral triangle made of paper bends in a straight line so that
one of the vertices falls on the opposite side as shown on the picture.
Show that the corresponding angles of the two white triangles are
equal.