Problems

Let \(C_1\) and \(C_2\) be two concentric circles with \(C_1\) inside \(C_2\) and the center \(A\). Let \(B\) and \(D\) be two points on \(C_1\) that are not diametrically opposite. Extend the segment \(BD\) past \(D\) until it meets the circle \(C_2\) in \(C\). The tangent to \(C_2\) at \(C\) and the tangent to \(C_1\) at \(B\) meet in a point \(E\). Draw from \(E\) the second tangent to \(C_2\) which meets \(C_2\) at the point \(F\). Show that \(BE\) bisects angle \(\angle FBC\).

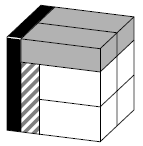
Michael made a cube with edge \(1\) out of eight bars as in the picture. All \(8\) bars have the same volume. The dimensions of the grey bars are the same as each other. Similarly, the dimensions of the white bars are the same as each other. Find the lengths of the edges of the white bars.

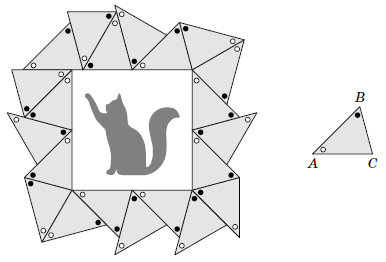
Peter went to the Museum of Modern Art and saw a square painting in a frame of an unusual shape. The frame consisted of \(21\) congruent triangles. Peter was interested in what the angles of these triangles were equal to. Help him find these angles.

Let \(A\), \(B\), \(C\) and \(D\) be four points labelled clockwise on the circumference of a circle. The diagonals \(AC\) and \(BD\) intersect at the centre \(O\) of the circle. What can be deduced about the quadrilateral \(ABCD\)?

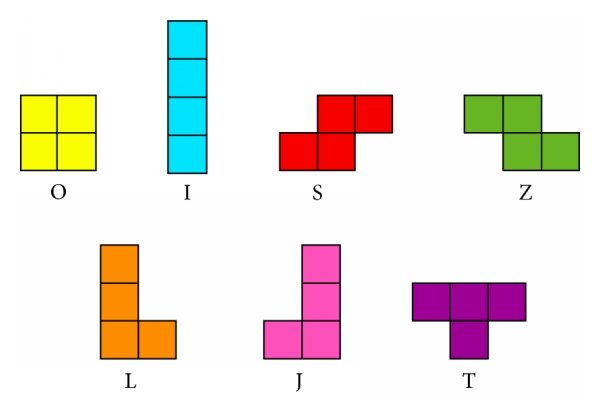
Consider the 7 different tetrominoes. Is it possible to cover a \(4\times7\) rectangle with exactly one copy of each of the tetrominoes? If it is possible, then provide an example layout. If it is not possible, then prove that it’s impossible.

We allow rotation of the tetrominoes, but not reflection. This means that we consider \(S\) and \(Z\) as different, as well as \(L\) and \(J\).

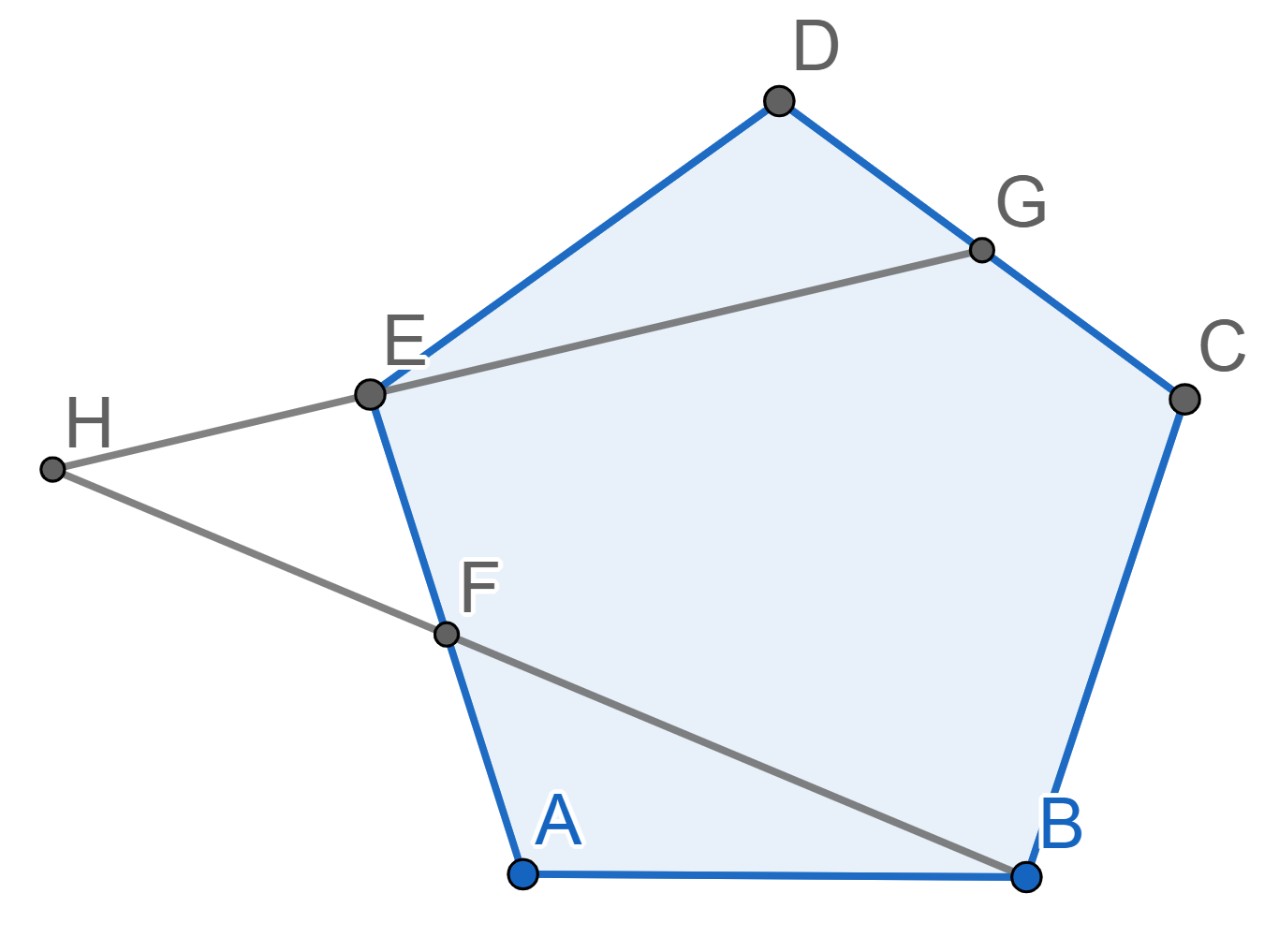
Let \(ABCDE\) be a regular pentagon. The point \(G\) is the midpoint of \(CD\), the point \(F\) is the midpoint of \(AE\). The lines \(EG\) and \(BF\) intersect at the point \(H\). Find the angle \(EHF\).

A paper band of constant width is tied into a simple knot and tightened. Prove that the knot has the shape of a regular polygon.

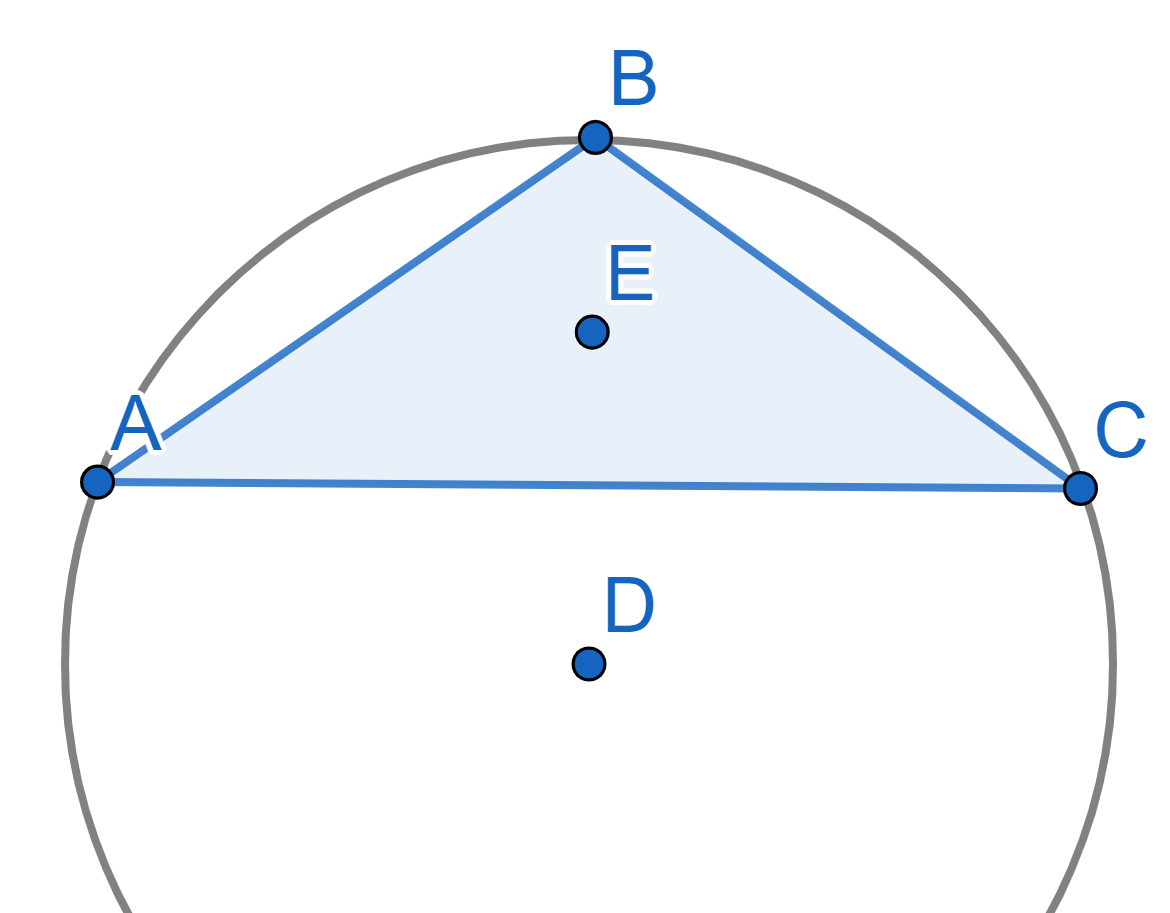
\(ABC\) is a triangle. The circumscribed circle is the circle that touches all three vertices of the triangle \(ABC\). It is also the smallest circle lying entirely outside the triangle. The center of the circumscribed circle is \(D\).

The inscribed circle is the circle which touches all three sides of the triangle \(ABC\). It is also the largest circle lying entirely inside the triangle. The center of the inscribed circle is \(E\).

The points \(D\) and \(E\) are symmetric with respect to the segment \(AC\). Find the angles of the triangle \(ABC\).

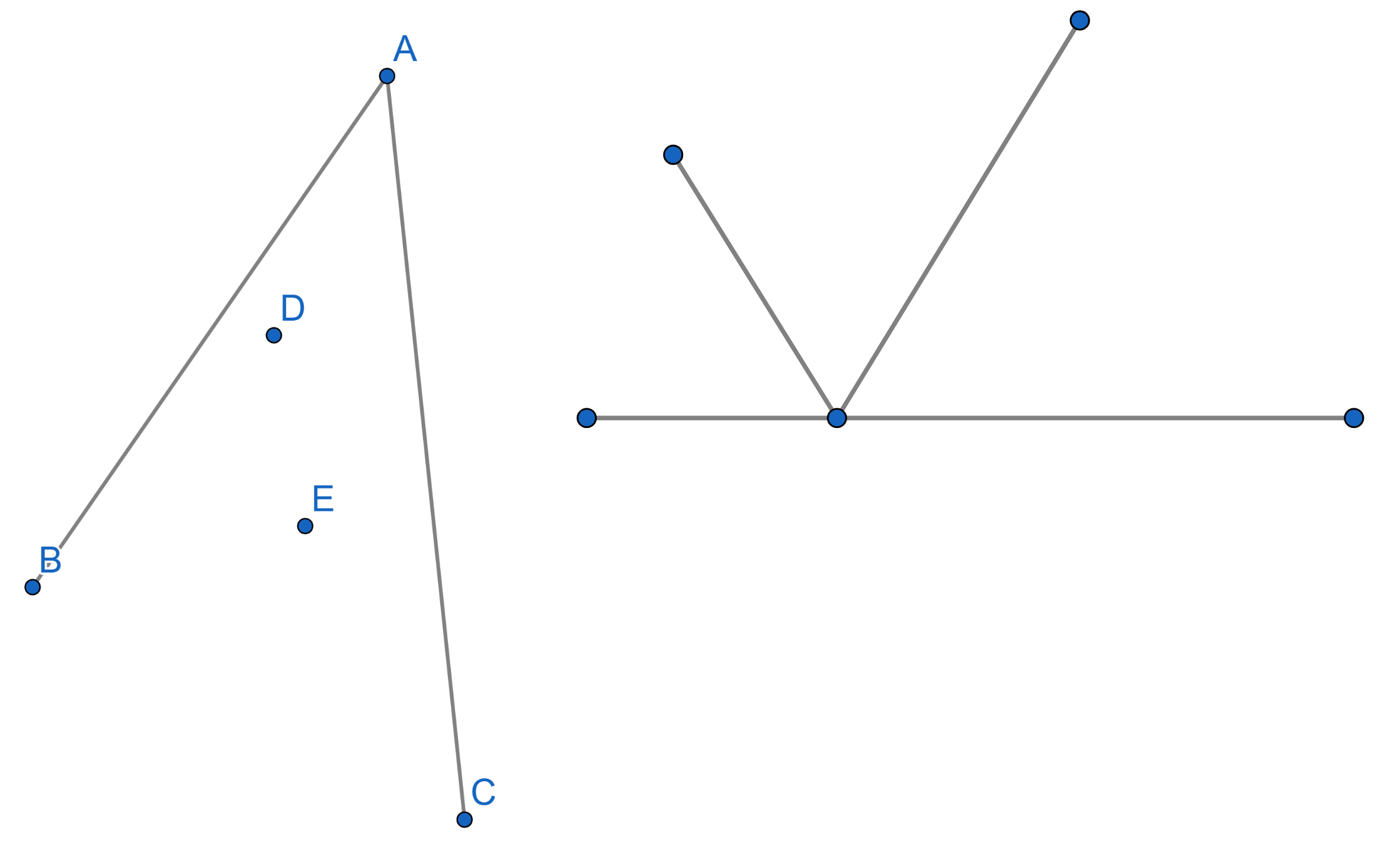
Between two mirrors \(AB\) and \(AC\), forming a sharp angle two points \(D\) and \(E\) are located. In what direction should one shine a ray of light from the point \(D\) in such a way that it would reflect off both mirrors and hit the point \(E\)?
If a ray of light comes towards a surface under a certain angle, it is reflected with the same angle as on the picture.

Let \(a\), \(b\) and \(c\) be the three side lengths of a triangle. Does there exist a triangle with side lengths \(a+1\), \(b+1\) and \(c+1\)? Does it depend on what \(a\), \(b\) and \(c\) are?