Problems

In the triangle \(ABC\) with a right angle \(\angle ACB\), \(CD\) is the height and \(CE\) is the bisector. Draw the bisectors \(DF\) and \(DG\) of the triangles \(BDC\) and \(ADC\). Prove that \(CFEG\) is a square.

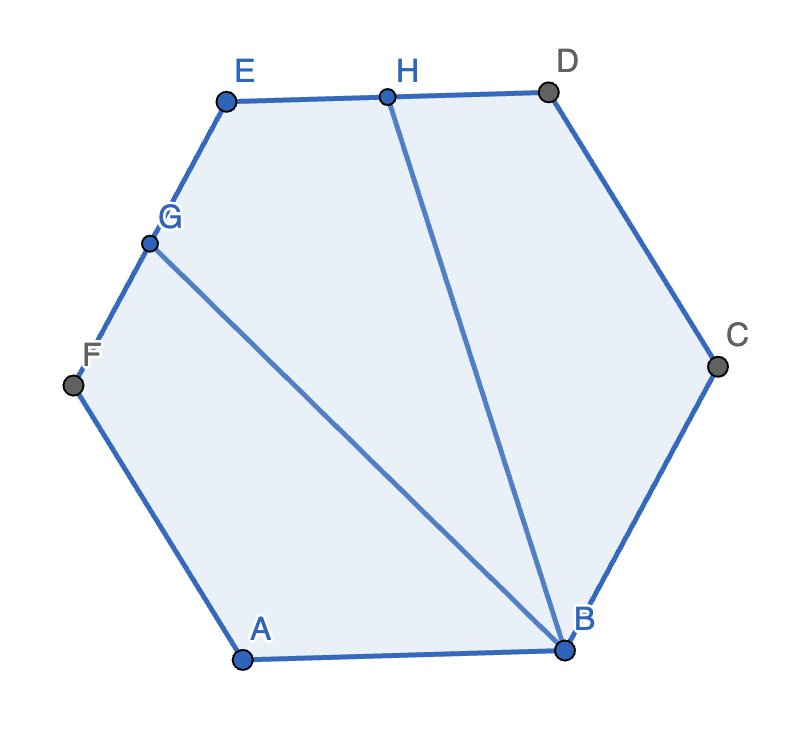
Let \(ABCDEF\) be a regular hexagon. Points \(G\) and \(H\) lie on \(EF\) and \(DE\) respectively such that \(|EG|=|EH|\). Furthermore, the area of quadrilateral \(ABGF\) is equal to the area of quadrilateral \(BGEH\), which are both equal to the area of \(BCDH\). What’s the ratio \(\frac{|EG|}{|EF|}\)?

Let \(ABCD\) be a square and let \(X\) be any point on side \(BC\) between \(B\) and \(C\). Let \(Y\) be the point on line \(CD\) such that \(BX=YD\) and \(D\) is between \(C\) and \(Y\). Prove that the midpoint of \(XY\) lies on diagonal \(BD\).

Let \(ABCD\) be a trapezium such that \(AB\) is parallel to \(CD\). Let \(E\) be the intersection of diagonals \(AC\) and \(BD\). Suppose that \(AB=BE\) and \(AC=DE\). Prove that the internal angle bisector of \(\angle BAC\) is perpendicular to \(AD\).

Let \(ABC\) be an isosceles triangle with \(AB=AC\). Point \(D\) lies on side \(AC\) such that \(BD\) is the angle bisector of \(\angle ABC\). Point \(E\) lies on side \(BC\) between \(B\) and \(C\) such that \(BE=CD\). Prove that \(DE\) is parallel to \(AB\).

\(ABCD\) is a rectangle with side lengths \(AB=CD=1\) and \(BC=DA=2\). Let \(M\) be the midpoint of \(AD\). Point \(P\) lies on the opposite side of line \(MB\) to \(A\), such that triangle \(MBP\) is equilateral. Find the value of \(\angle PCB\).

A rectangular sheet of paper is folded so that one corner lies on top of the corner diagonally opposite. The resulting shape is a pentagon whose area is \(20\%\) one-sheet-thick, and \(80\%\) two-sheets-thick. Determine the ratio of the two sides of the original sheet of paper.

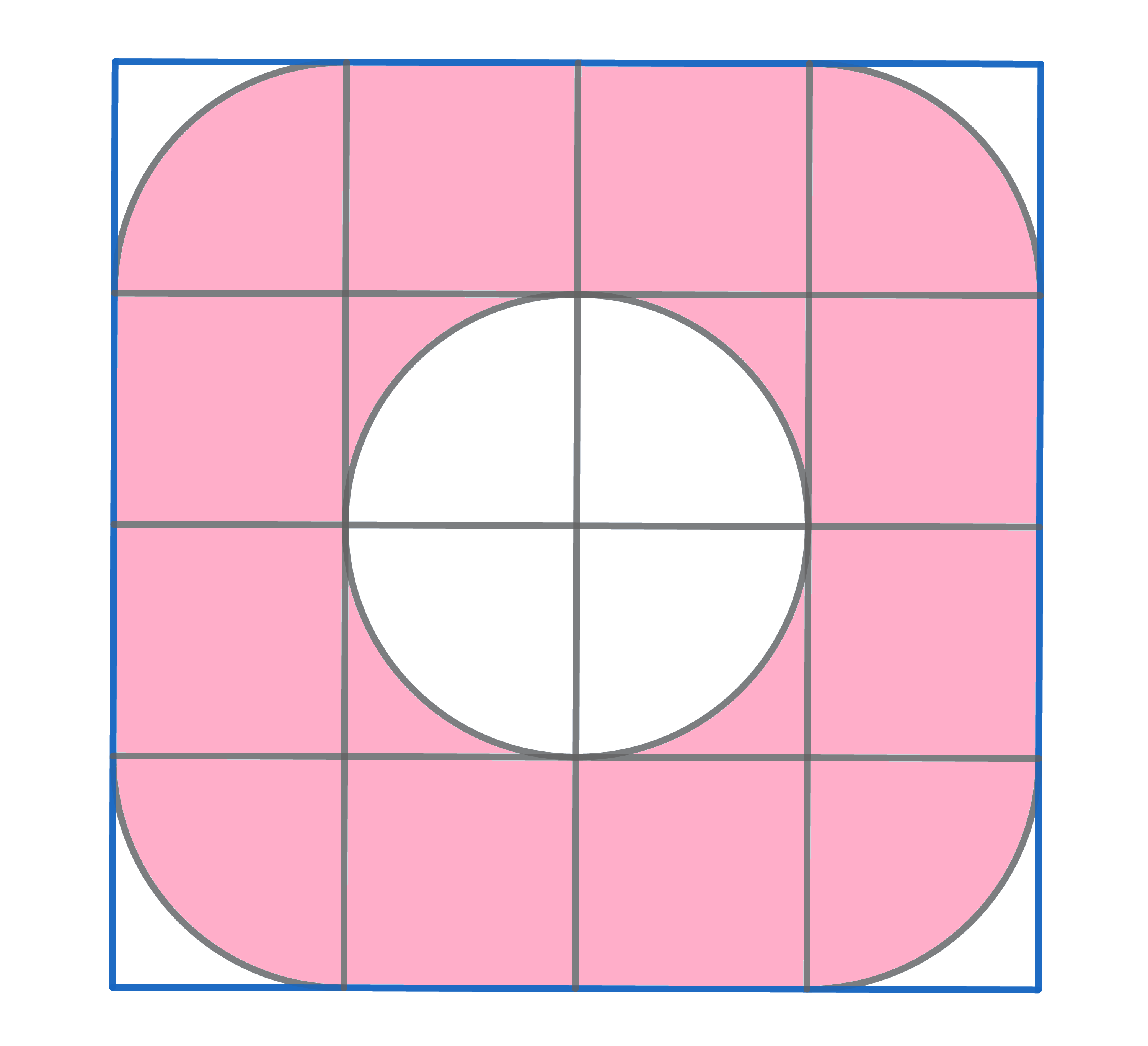
The area of the coloured figure equals \(48\)cm\(^2\). Find the length of the side of the smallest square.

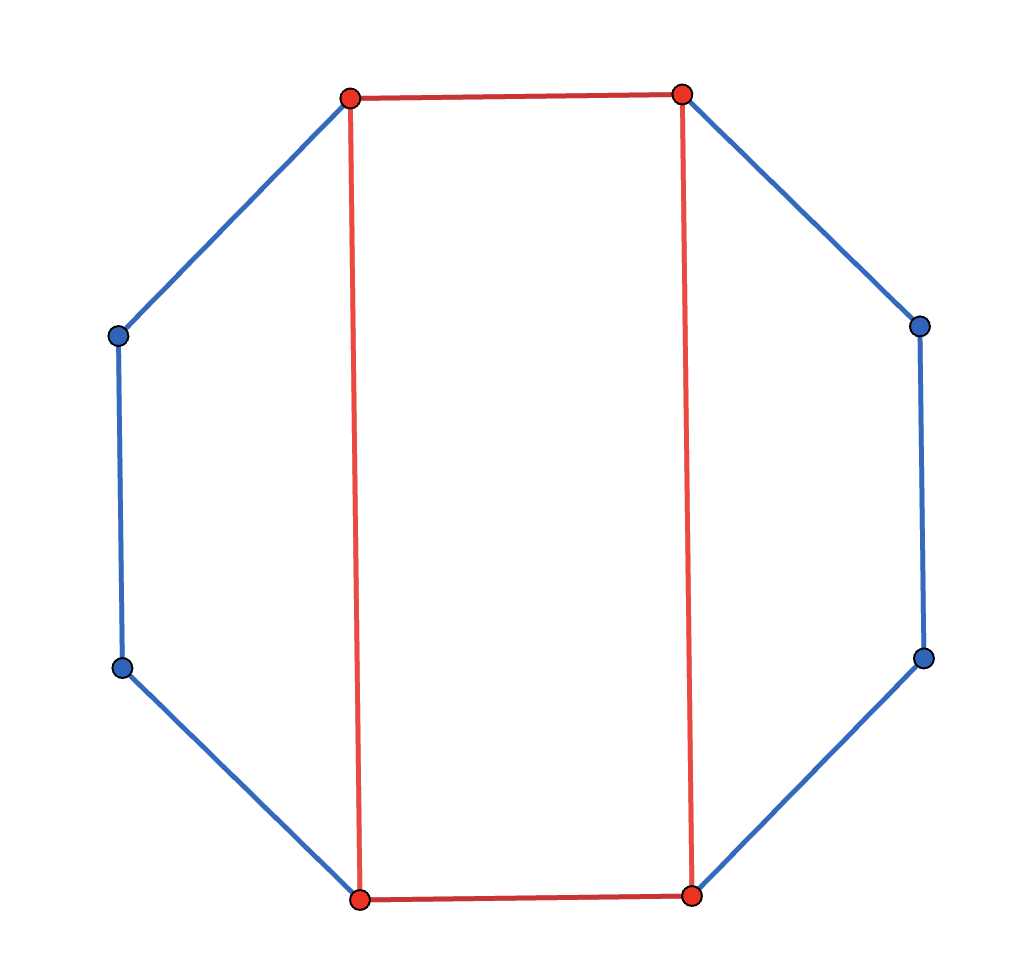
Below is a regular octagon. Given that its side length is \(1\), what’s the difference between the area of the red rectangle and the rest of the octagon?

In the diagram, all the small squares are of the same size. What fraction of the large square is shaded?