Problems

What symmetries does a regular hexagon have, and how many?

Let \(X\) be a finite set, and let \(\mathcal{P}X\) be the power set of \(X\) - that is, the set of subsets of \(X\). For subsets \(A\) and \(B\) of \(X\), define \(A*B\) as the symmetric difference of \(A\) and \(B\) - that is, those elements that are in either \(A\) or \(B\), but not both. In formal set theory notation, this is \(A*B=(A\cup B)\backslash(A\cap B)\).

Prove that \((\mathcal{P}X,*)\) forms a group.

The lengths of three sides of a right-angled triangle are all integers.

Show that one of them is divisible by \(5\).

You have a row of coins and you can perform these three operations as many times as you like:

1. Remove three adjacent heads

2. Remove two adjacent tails

3. If there’s a tail followed by a heads, then turn the tail over and put a new tail after both heads

You apply these operations until you can’t make any more moves. Show that you will always get the same configuration at the end, no matter the order.

Let \(a\) be a positive integer, and let \(p\) be a prime number. Prove that \(a^p - a\) is a multiple of \(p\).

We ‘typically’ use the formula \(\frac{1}{2}bh\) for the area of a triangle, where \(b\) is the length of the base, and \(h\) is the perpendicular height. Here’s another one, called Heron’s formula.

Call the sides of the triangle \(a\), \(b\) and \(c\). The perimeter is \(a+b+c\). We call half of this the semiperimeter, \(s=\frac{a+b+c}{2}\). Then the area of this triangle is \[\sqrt{s(s-a)(s-b)(s-c)}.\] Prove this formula is correct.

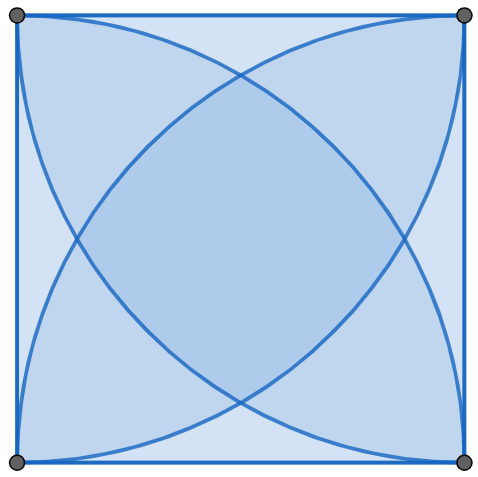
We have a square of side length 1. At each vertex of the square, we draw a circle of radius 1. What is the area bounded by all four circles?

A simple polygon is a polygon that does not intersect itself and has no holes. Suppose we have a simple polygon \(S\) whose vertices consists of only integer coordinates.

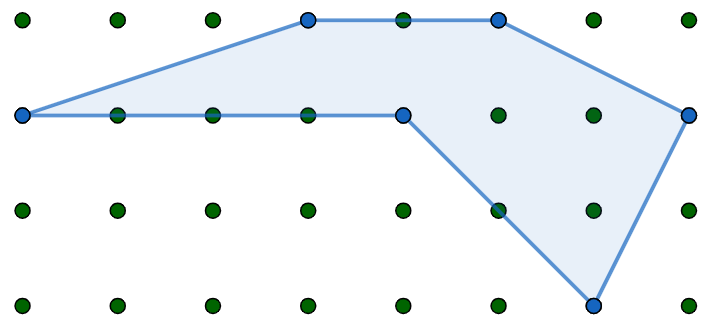
The area turns out to be remarkably easy to calculate. Count up the number of points with integer coordinate inside the polygon and on the boundary; call them \(i\) and \(b\) respectively. The area is then \[A(S) = i+\frac{b}{2}-1.\]

In the picture above, \(i=3\) and \(b=11\), so \(A(S) = \frac{15}{2}\). Prove that this formula for the area \(A(S)\) is correct.

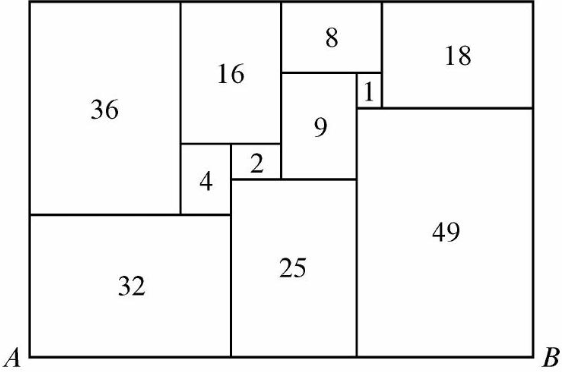
All of the rectangles in the figure below, which is drawn to scale, are similar to the big rectangle (that is, their sides are in the same ratio). Each number represents the area of the rectangle. What is the length \(AB\)?

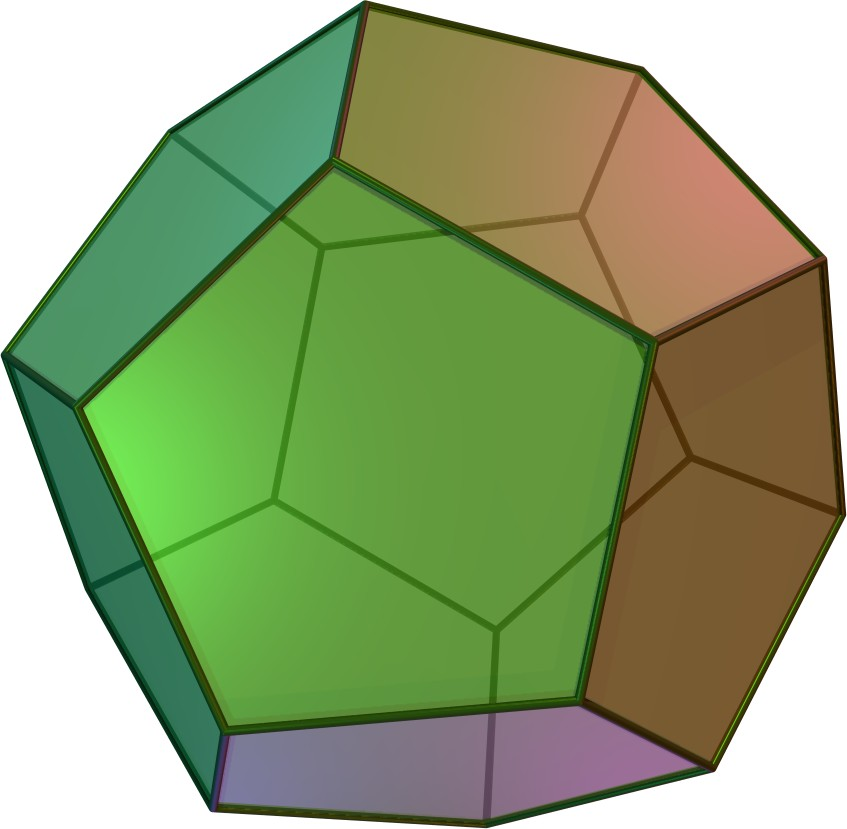
Take a regular dodecahedron as in the image. It has \(12\) regular pentagons as its faces, \(30\) edges, and \(20\) vertices. We can cut it with planes in various ways and the cut will be a polygon on a plane. Find out how many ways there are to cut a dodecahedron with a plane so that the polygon obtained is a regular hexagon.