Problems
The perimeter of the triangle \(\triangle ABC\) is \(10\). Let \(D,E,F\) be the midpoints of the segments \(AB,BC,AC\) respectively. What is the perimeter of \(\triangle DEF\)?
Let \(\triangle ABC\) be a triangle and \(D\) be a point on the edge \(BC\) so that the segment \(AD\) bisects the angle \(\angle BAC\). Show that \(\frac{|AB|}{|BD|}=\frac{|AC|}{|CD|}\).
The volume of a pyramid is \(\frac{1}{3}Bh\), where \(B\) is the area of the base and \(h\) is the perpendicular height. What’s the volume of a regular tetrahedron with side length \(1\)?
The Great Pyramid of Giza is the largest pyramid in Egypt. For the purposes of this problem, assume that it’s a perfect square-based pyramid, with perpendicular height \(140\)m and the square has side length \(230\)m.
What is its volume in cubic metres?
A regular octahedron is a solid with eight faces, all of which are equilateral triangles. It can be formed by placing together two square based pyramids at their bases.
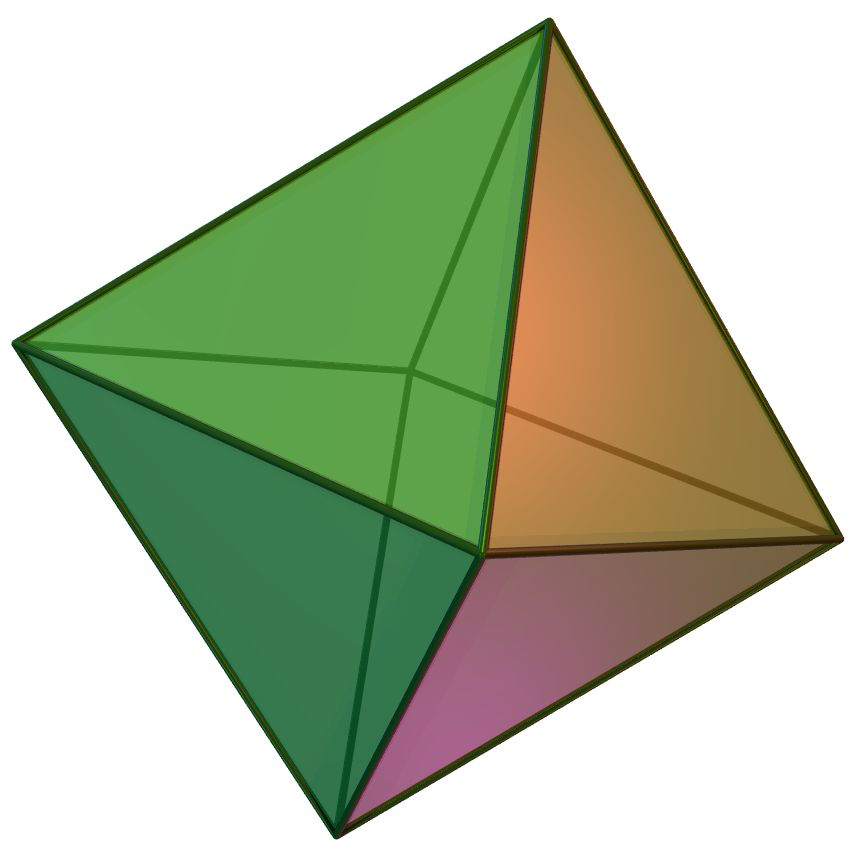
What is the volume of an octahedron with side length \(1\)?
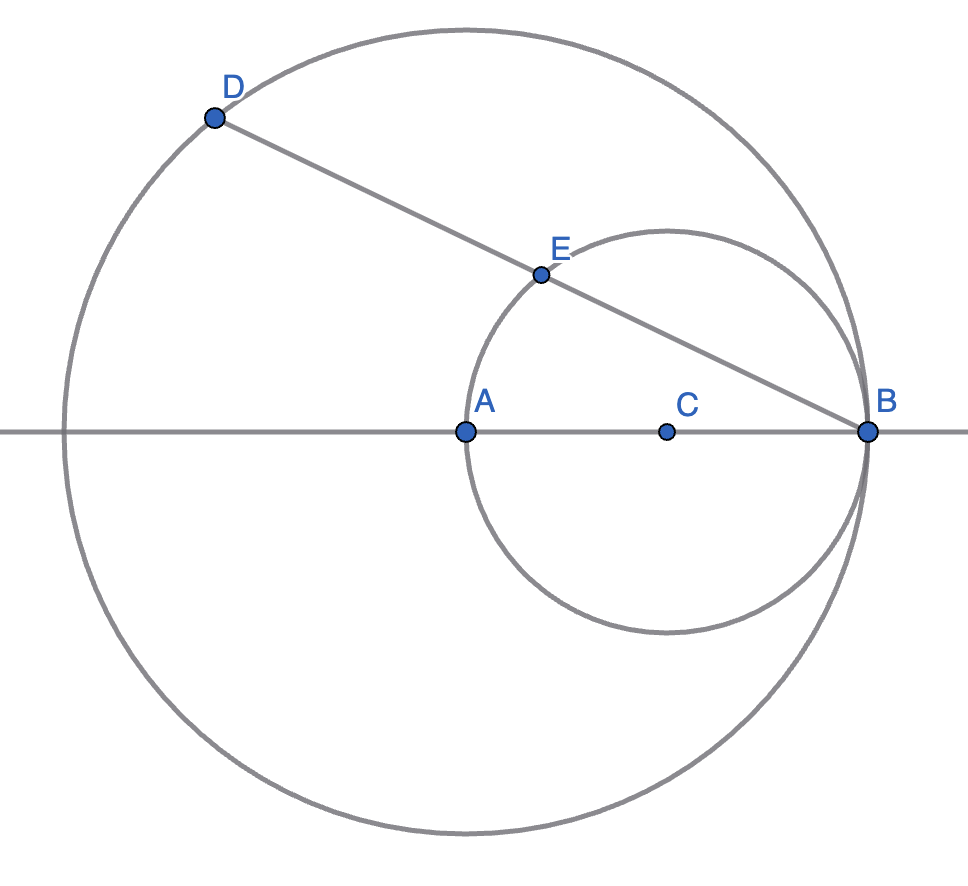
A circle with centre \(A\) has the point \(B\) on its circumference. A smaller circle is drawn inside this with \(AB\) as a diameter and \(C\) as its centre. A point \(D\) (which is not \(B\)) is chosen on the circumference of the bigger circle, and the line \(BD\) is drawn. \(E\) is the point where the line \(BD\) intersects the smaller circle.
Show that \(|BE|=|DE|\).
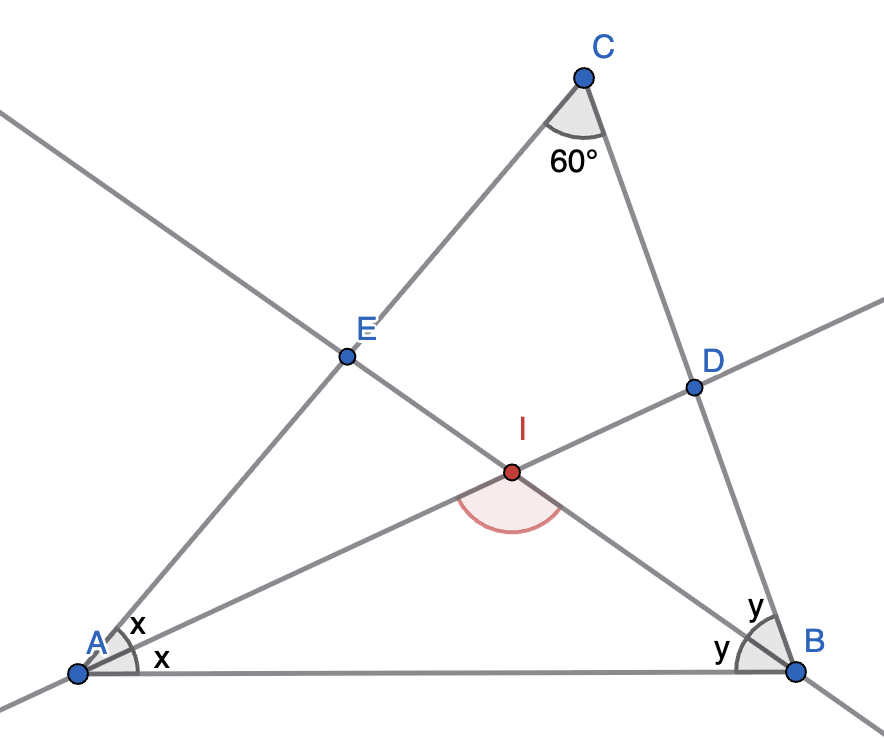
In the triangle \(\triangle ABC\), the angle \(\angle ACB=60^{\circ}\), marked at the top. The angle bisectors \(AD\) and \(BE\) intersect at the point \(I\).
Find the angle \(\angle AIB\), marked in red.
Without using any wolves, show that Robinson’s goat can only graze shapes that are convex (that means, whenever you pick two points inside the shape, the whole line between them also lies inside). But if Robinson is allowed to use as many wolves as he likes, this restriction disappears. Show that in this case, he can make the goat graze in the shape of any polygon at all.
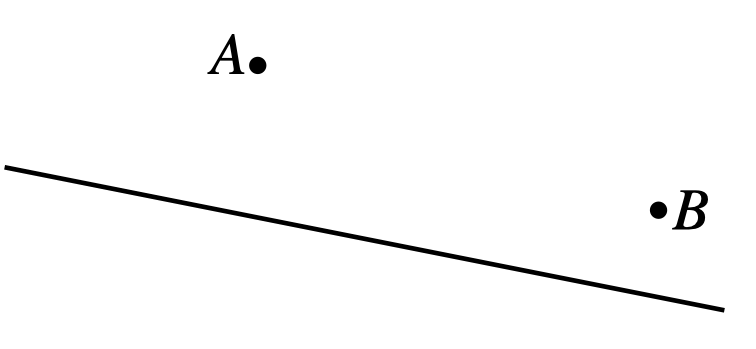
Fred starts running from point \(A\) and must reach point \(B\). On the way, he has to touch the fence shown as a straight line in the figure. It doesn’t matter where he touches the fence, as long as he does. What is the shortest path he can take?