Problems
Robbie and Paloma are playing football on a large, flat field. They both run at the same speed toward the ball. Where could the ball have been if Paloma reached it first?
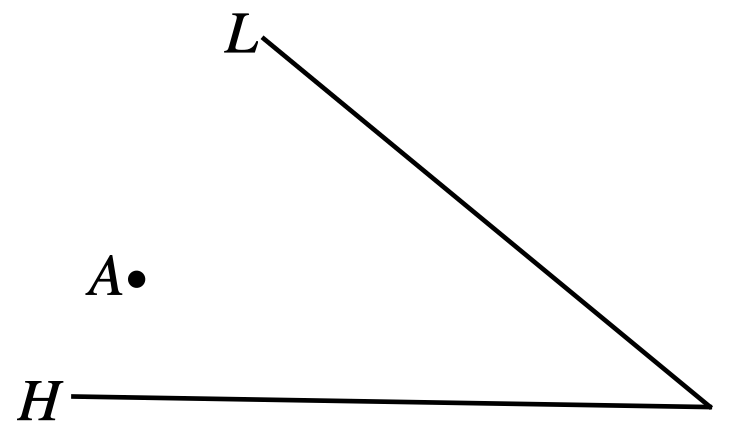
Oliver starts running from point \(A\) in the figure below. He must touch line \(H\), and then line \(L\). What is the shortest path he can take?
Two ants move along the same straight line and can only move back and forth along it. The first ant moves twice as fast as the second. Where could you place a breadcrumb so that the slower ant reaches it first?
Two ants, Muffy and Chip, start on opposite sides of a circle. Muffy moves twice as fast as Chip, and both can only move along the circle’s edge. Where could a breadcrumb be placed so that they both reach it at the same time?
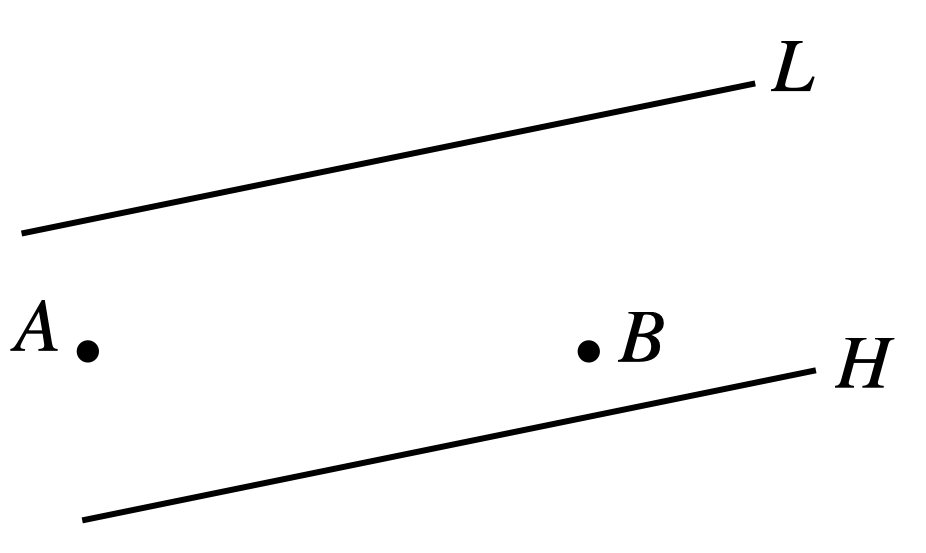
Two points, \(A\) and \(B\), lie between two lines \(L\) and \(H\). Draw the shortest path from \(A\) to \(B\) that touches \(L\), then \(H\), and finally reaches \(B\).
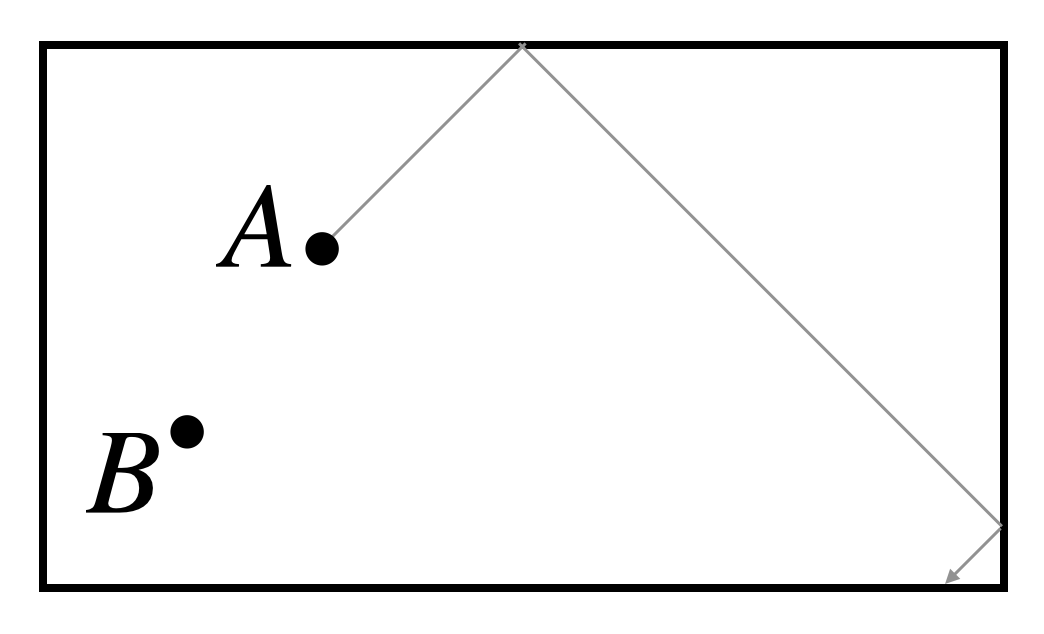
Ignat is playing pool and places a ball at point \(A\), as shown below. Can he bounce ball \(A\) off a ball placed at position \(B\), if the ball can only bounce off the top and right edges of the pool table?
When a ball bounces off the edge, it does so just like light reflecting in a mirror: the angle at which it hits the edge is the same as the angle at which it bounces away.
A ball \(A\) is placed on the pool table as shown below. The walls are labeled as follows: wall \(1\) is the top wall, wall \(2\) is the right wall, wall \(3\) is the bottom wall, and wall \(4\) is the left wall.
If we hit the ball so that it bounces off the walls labeled \(1\), \(2\), \(3\), and \(4\) —in that order—and then stops rolling just before hitting the next wall, what region of the pool table can the ball reach? If the ball hits a corner, it also stops.
A point \(P\) and a line \(L\) are drawn on a piece of paper. What is the shortest path from \(P\) to \(L\)? You should give a proof that your path is indeed the shortest.
In Problemtown there are \(n\) farms and also \(n\) wells which we think of as points on a plane. We know that no three points lie on a straight line. The mayor wants to build straight roads so that each farm is connected to exactly one well, and each well is connected to exactly one farm. The mayor insists that no two roads are allowed to cross each other. Prove that this is always possible.
An airplane is flying from Prague to Tokyo, which are cities in the northern hemisphere with different latitudes. Suppose that the airplane must touch the equator. Could you help the pilot find the shortest path that the airplane can take, assuming that the Earth is a perfect sphere?