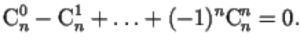Problems
What is the maximum number of pairwise non-parallel segments with endpoints at the vertices of a regular \(n\)-gon?
Prove that it is not possible to completely cover an equilateral triangle with two smaller equilateral triangles.
51 points were thrown into a square of side 1 m. Prove that it is possible to cover some set of 3 points with a square of side 20 cm.
a) An axisymmetric convex 101-gon is given. Prove that its axis of symmetry passes through one of its vertices.
b) What can be said about the case of a decagon?
In a country coming out of each city there are 100 roads and from each city it is possible to reach any other. One road was closed for repairs. Prove that even now you can get from every city to any other.
a) A piece of wire that is 120 cm long is given. Is it possible, without breaking the wire, to make a cube frame with sides of 10 cm?
b) What is the smallest number of times it will be necessary to break the wire in order to still produce the required frame?
Prove that out of \(n\) objects an even number of objects can be chosen in \(2^{n-1}\) ways.
Prove that every number \(a\) in Pascal’s triangle is equal to
a) the sum of the numbers of the previous right diagonal, starting from the leftmost number up until the one to the right above the number \(a\).
b) the sum of the numbers of the previous left diagonal, starting from the leftmost number to the one to left of the number which is above \(a\).
Prove that there exists a graph with 2n vertices whose degrees are \(1, 1, 2, 2, \dots , n, n\).