Problems

A square is cut by 18 straight lines, 9 of which are parallel to one side of the square and the other 9 parallel to the other – perpendicular to the first 9 – dividing the square into 100 rectangles. It turns out that exactly 9 of these rectangles are squares. Prove that among these 9 squares there will be two that are identical.

The population of China is one billion people. It would seem that on a map of China with a scale of 1 : 1,000,000 (1 cm : 10 km), it would be possible to fit a million times fewer people than there is in the whole country. However, in fact, not only 1000, but even 100 people will not be able to be placed on this map. Can you explain this contradiction?

In the triangle \(ABC\) the sides are compared as following: \(AC>BC>AB\). Prove that the angles are compared as follows: \(\angle B > \angle A > \angle C\).

Consider a quadrilateral \(ABCD\). Choose a point \(E\) on side \(AB\). A line parallel to the diagonal \(AC\) is drawn through \(E\) and meets \(BC\) at \(F\). Then a line parallel to the other diagonal \(BD\) is drawn through \(F\) and meets \(CD\) at \(G\). And then a line parallel to the first diagonal \(AC\) is drawn through \(G\) and meets \(DA\) at \(H\). Prove the \(EH\) is parallel to the diagonal \(BD\).

Cut an arbitrary triangle into parts that can be used to build a triangle that is symmetrical to the original triangle with respect to some straight line (the pieces cannot be inverted, they can only be rotated on the plane).

Let \(ABC\) and \(A_1B_1C_1\) be two triangles with the following properties: \(AB = A_1B_1\), \(AC = A_1C_1\), and angles \(\angle BAC = \angle B_1A_1C_1\). Then the triangles \(ABC\) and \(A_1B_1C_1\) are congruent. This is usually known as the “side-angle-side" criterion for congruence.

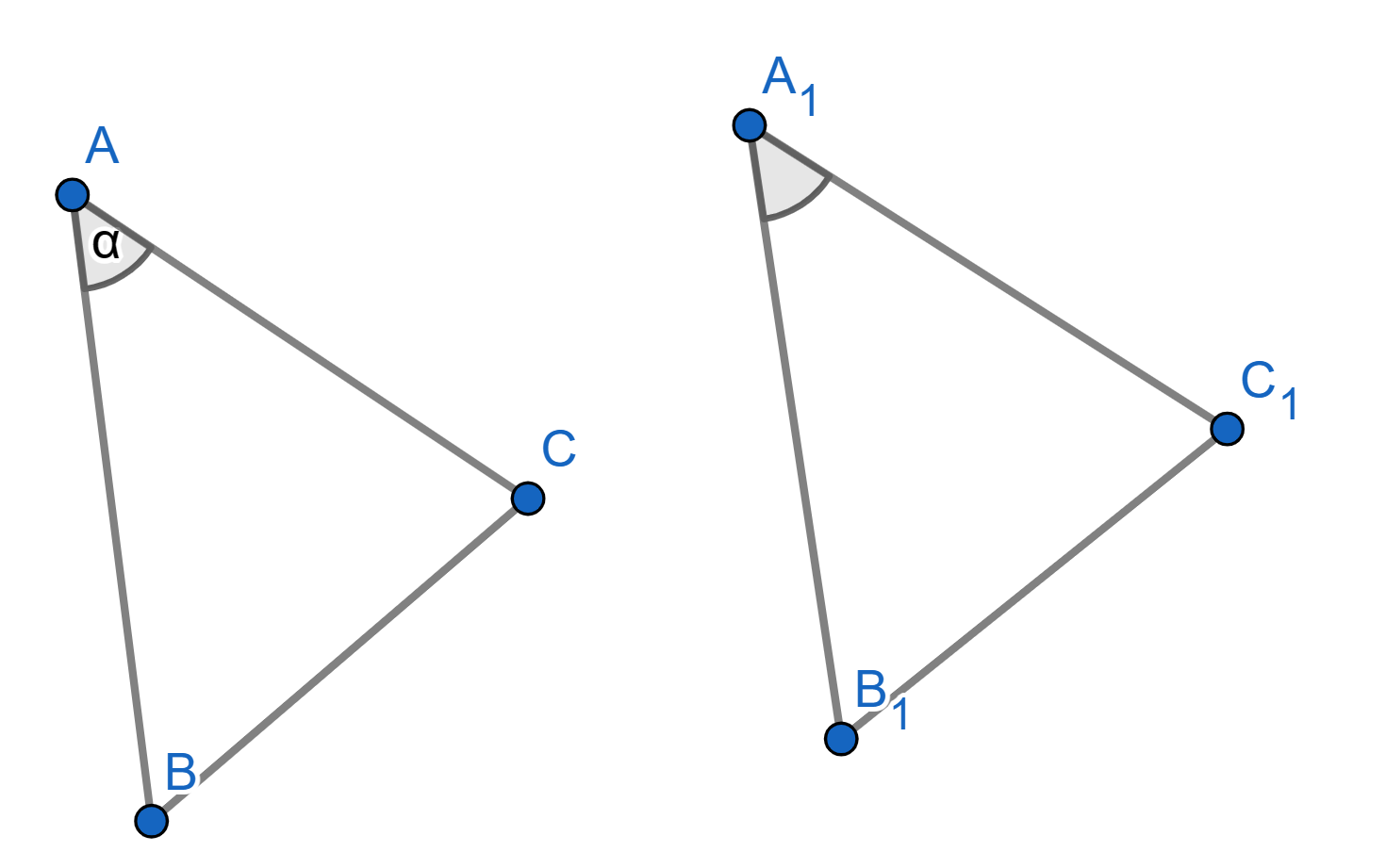
In the triangle \(\triangle ABC\) the sides \(AC\) and \(BC\) are equal. Prove that the angles \(\angle CAB\) and \(\angle CBA\) are equal.

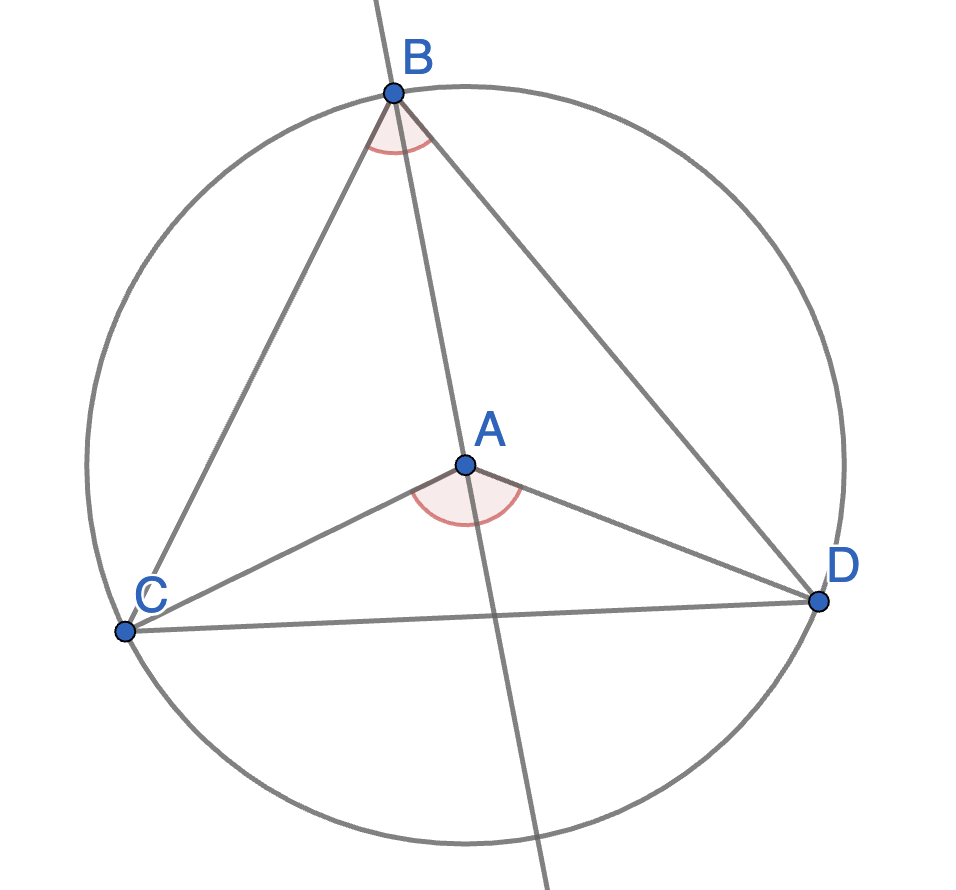
Point \(A\) is the centre of a circle and points \(B,C,D\) lie on that circle. The segment \(BD\) is a diameter of the circle. Show that \(\angle CAD = 2 \angle CBD\). This is a special case of the inscribed angle theorem.

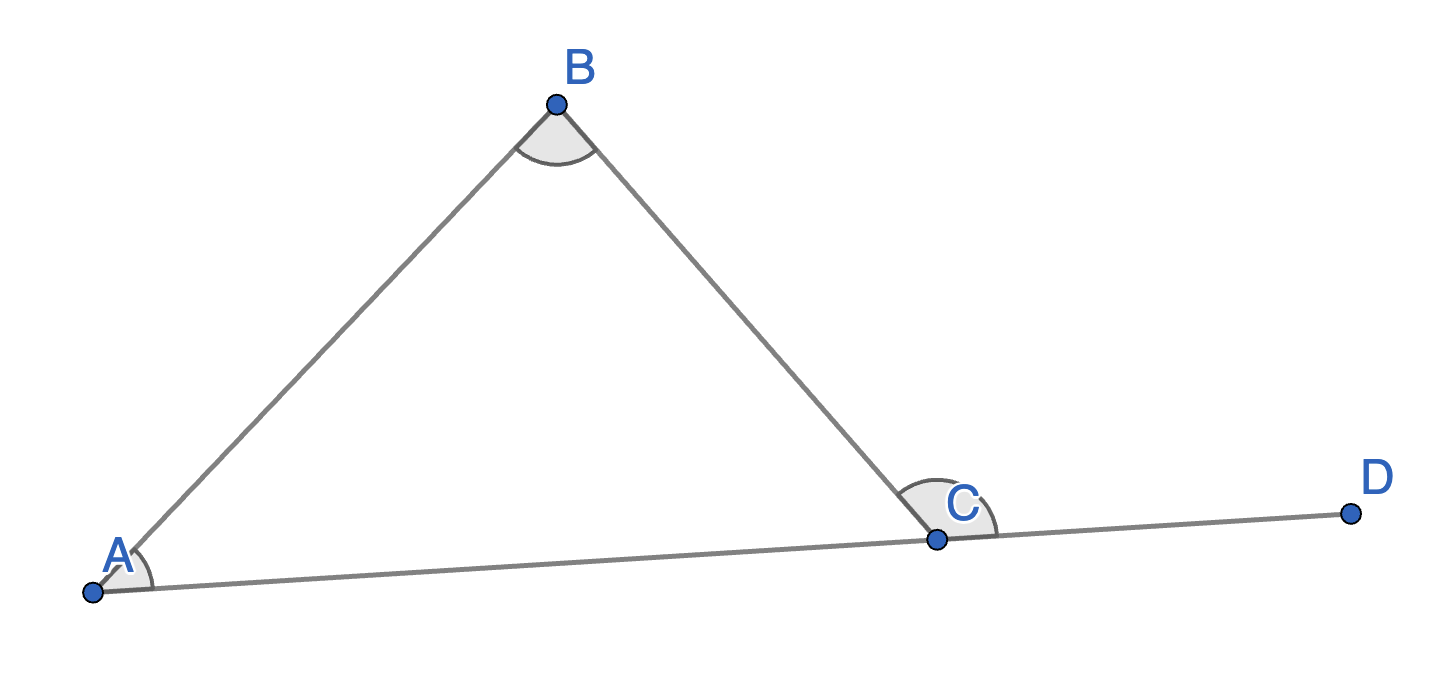
Let \(ABC\) be a triangle with given angles \(\angle BAC\) and \(\angle ABC\). What is the value of the angle \(\angle BCD\) in terms of \(\angle BAC\) and \(\angle ABC\)?

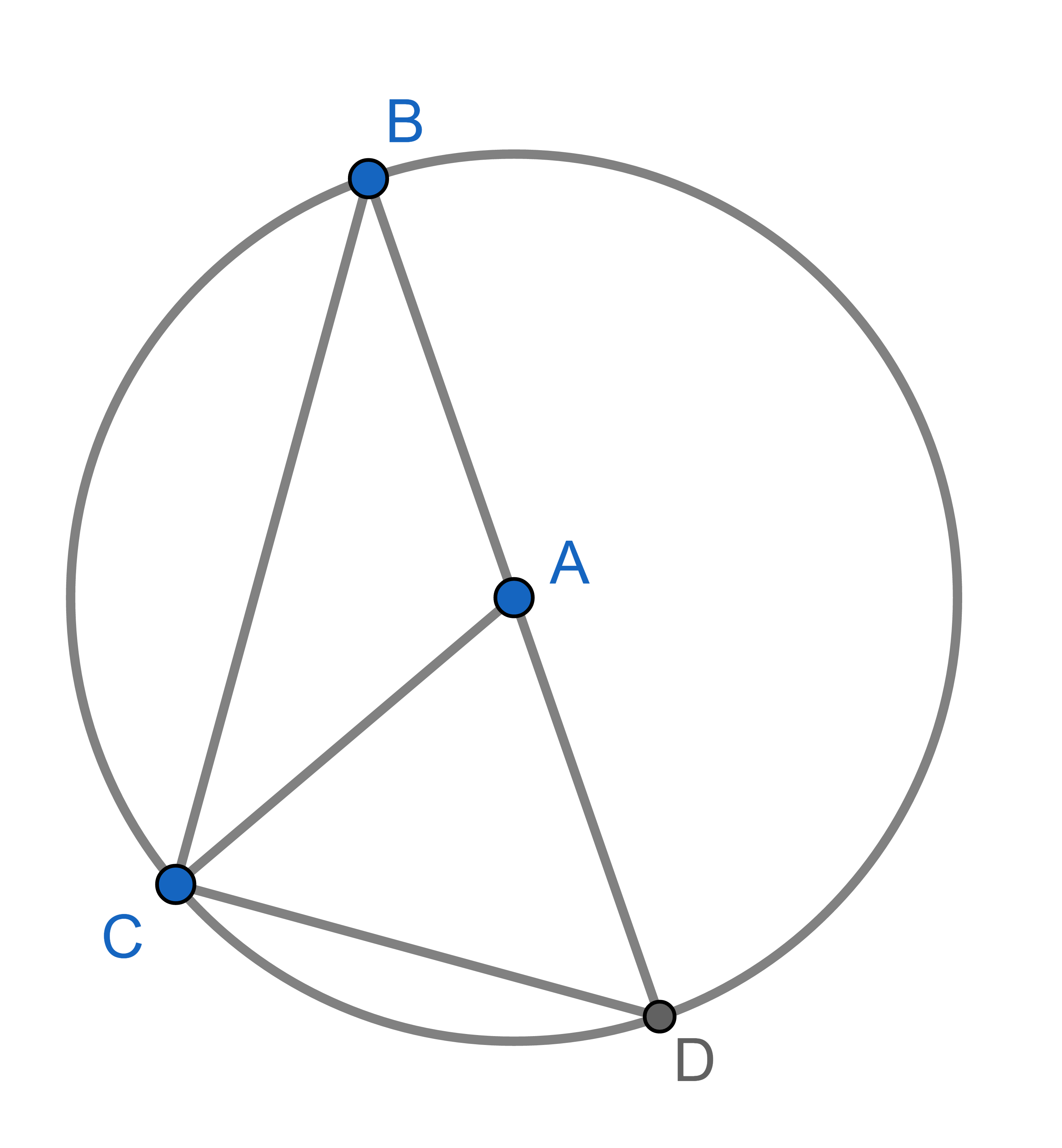
Point \(A\) is the centre of a circle and points \(B,C,D\) lie on that circle. Show that \(\angle CAD = 2 \angle CBD\). This statement is known as the inscribed angle theorem and is used widely in Euclidean geometry.