Problems

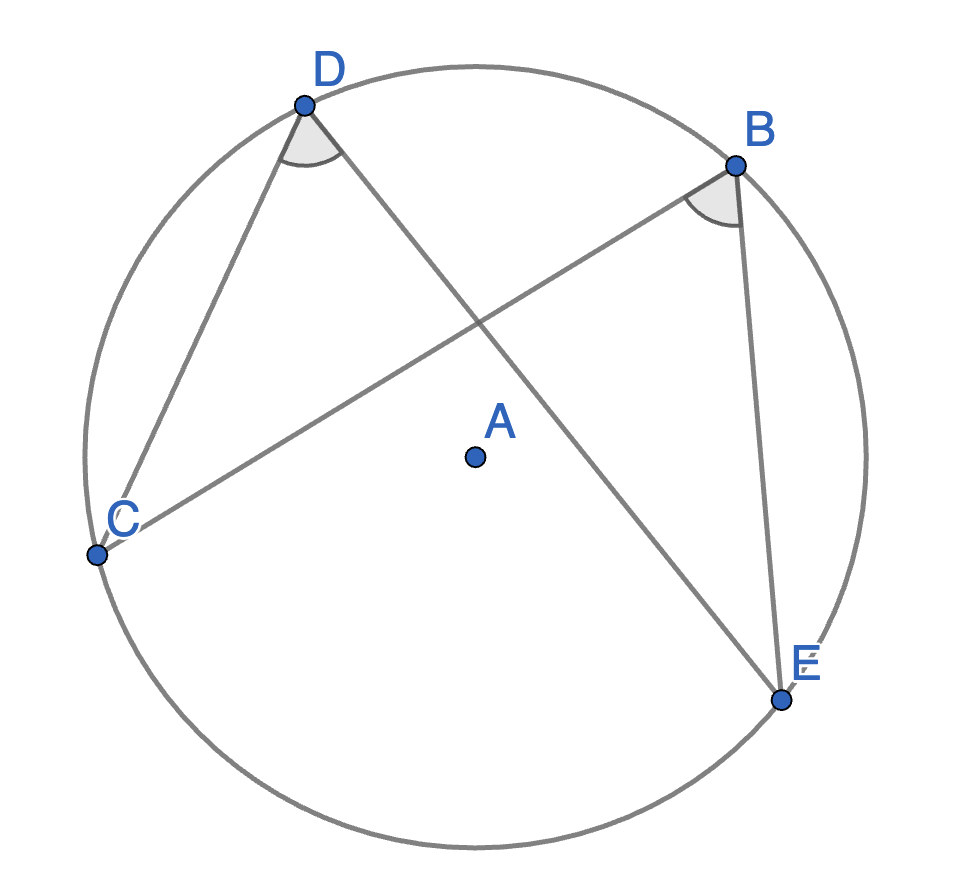
Let \(BCDE\) be a quadrilateral inscribed in a circle with centre \(A\). Show that angles \(\angle CDE\) and \(\angle CBE\) are equal. Also show that angles \(\angle BCD\) and \(\angle BED\) are equal. This says that all angles at the circumference subtended by the same arc are equal.

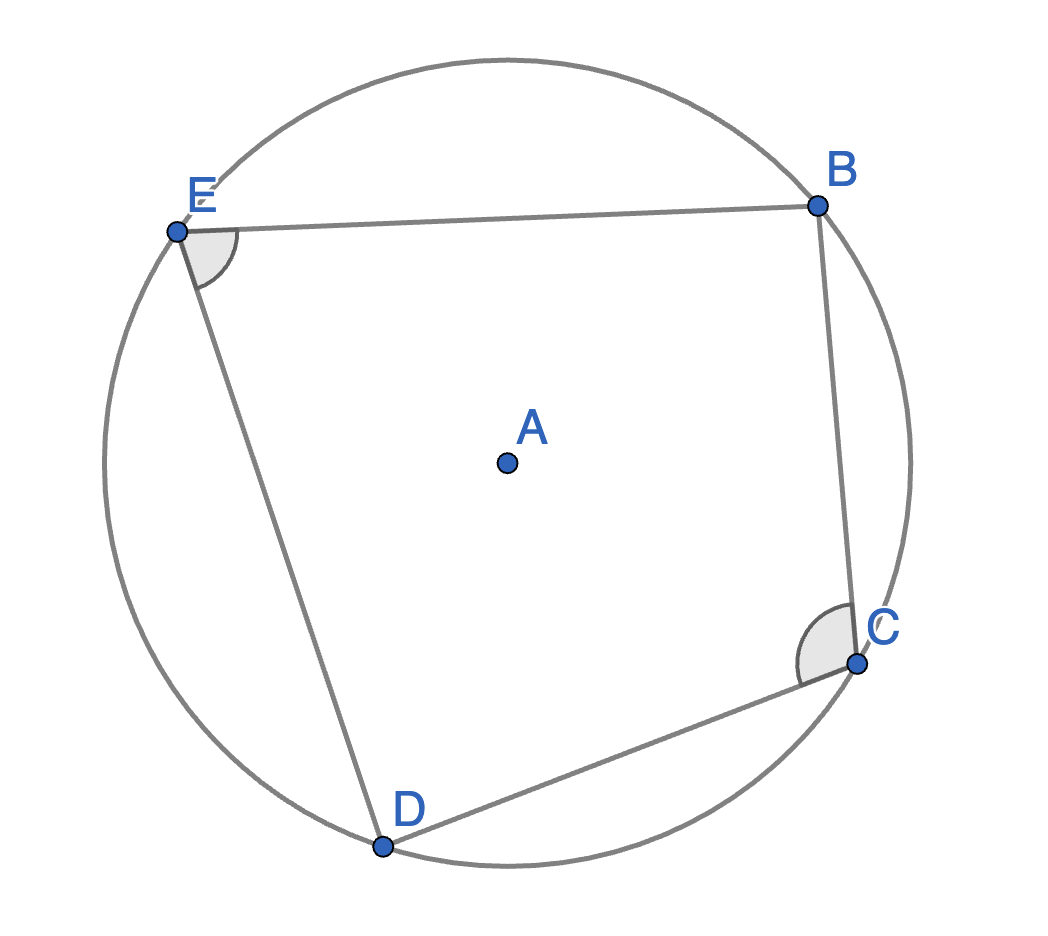
Let \(BCDE\) be an inscribed quadrilateral. Show that \(\angle BCD + \angle BED = 180^{\circ}\).

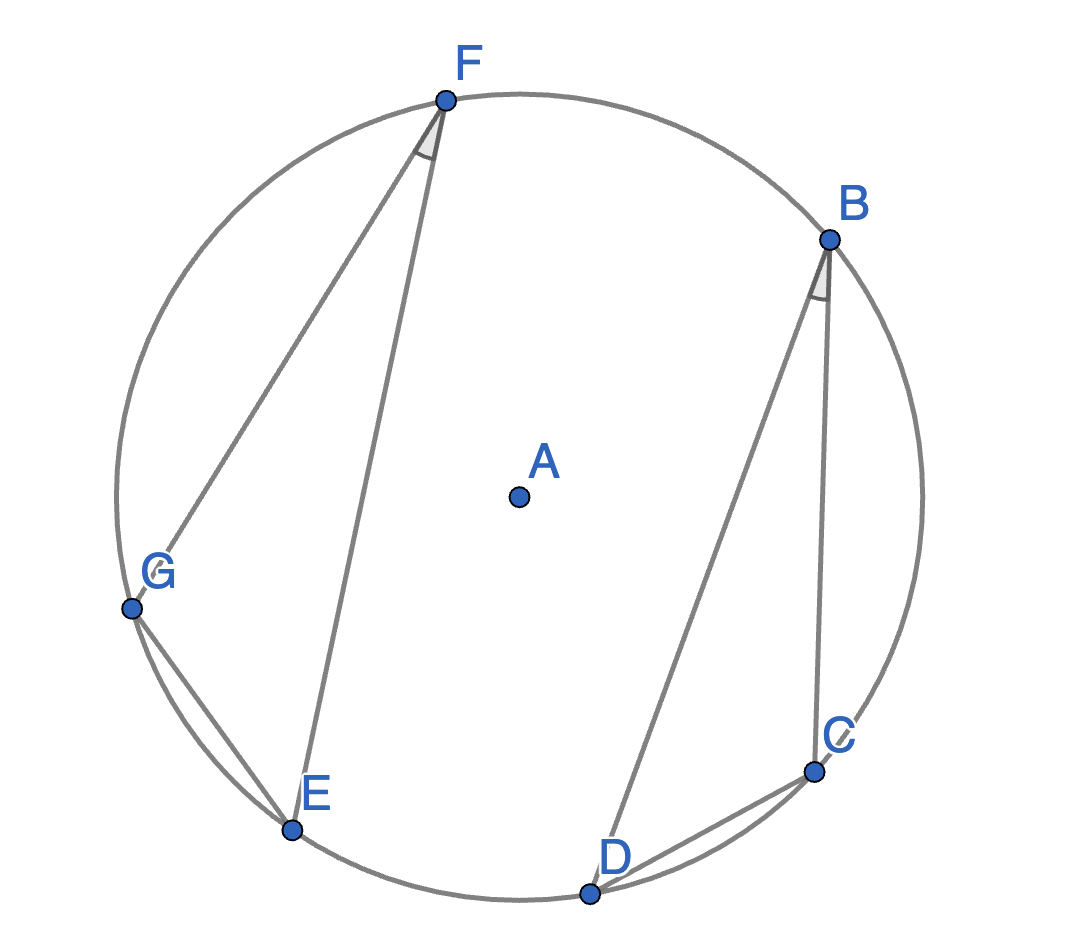
The points \(B\),\(C\),\(D\),\(E\),\(F\) and \(G\) lie on a circle with centre \(A\). The angles \(\angle CBD\) and \(\angle EFG\) are equal. Prove that the segments \(CD\) and \(EG\) have equal lengths.

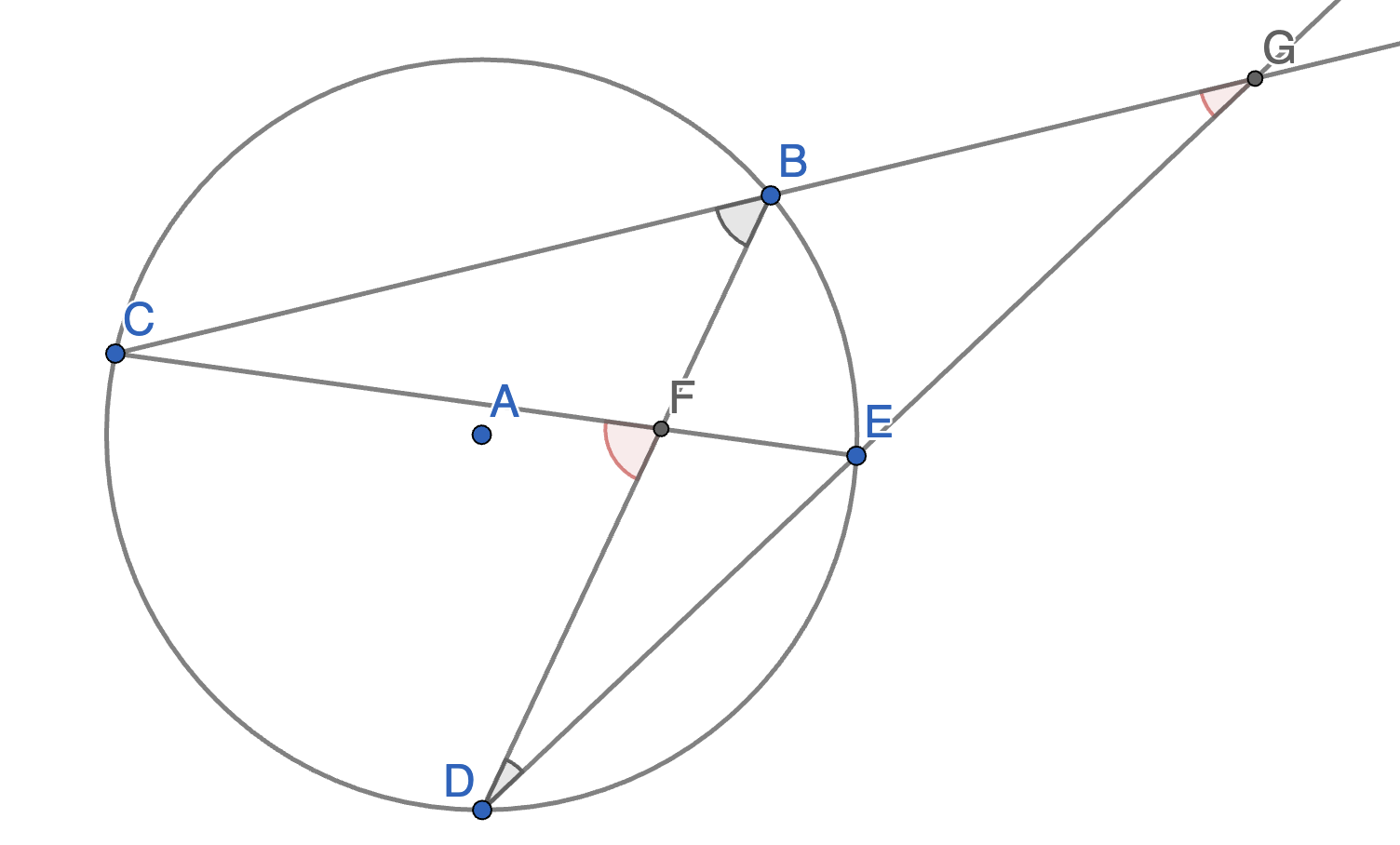
On the diagram below find the value of the angles \(\angle CFD\) and \(\angle CGD\) in terms of angles \(\angle CBD\) and \(\angle BDE\).

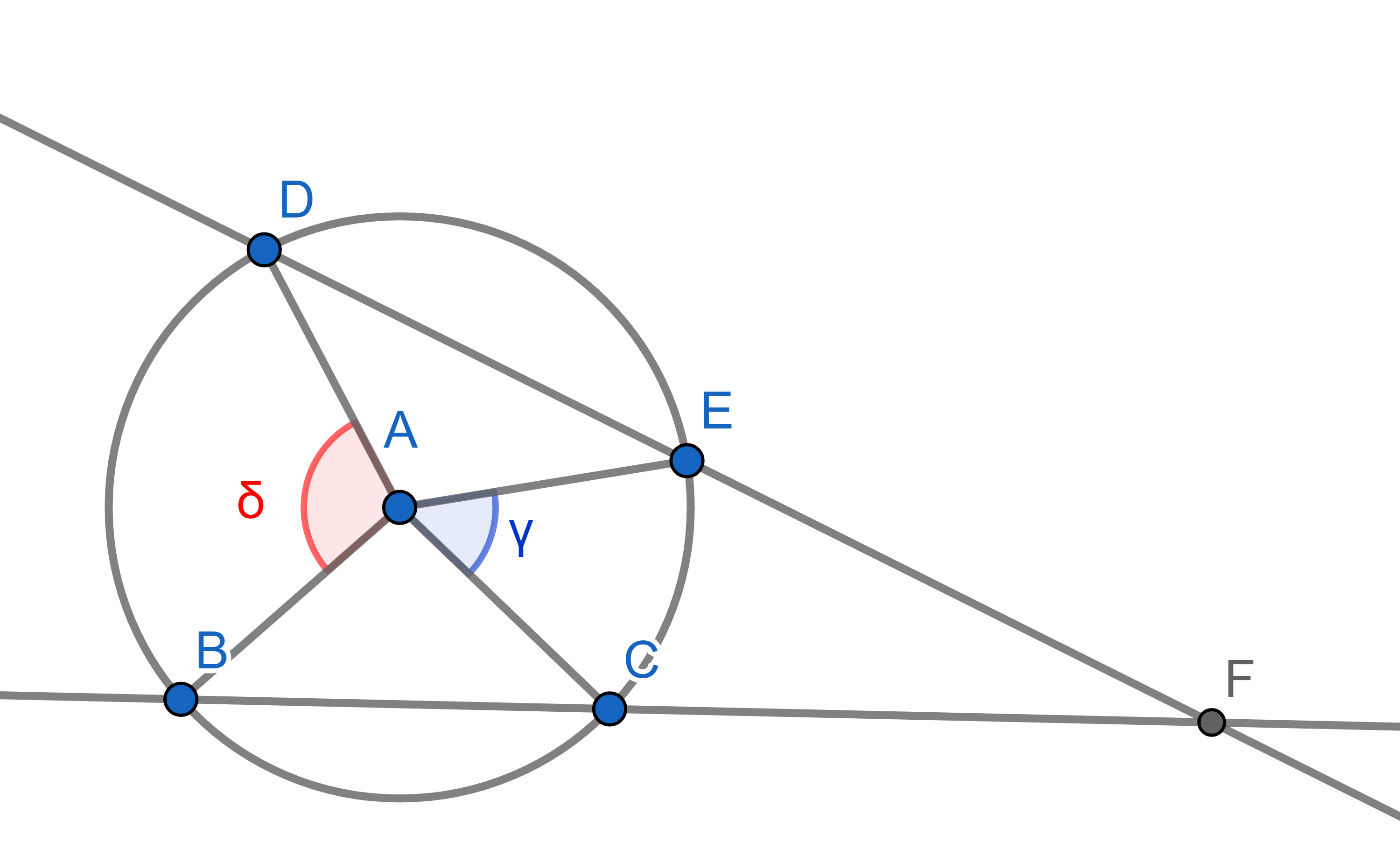
Point \(A\) is the centre of a circle. Points \(B,C,D,E\) lie on the circumference of this circle. Lines \(BC\) and \(DE\) cross at \(F\). We label the angles \(\angle BAD =\delta\) and \(\angle CAE = \gamma\). Express the angle \(DFB\) in terms of \(\gamma\) and \(\delta\).

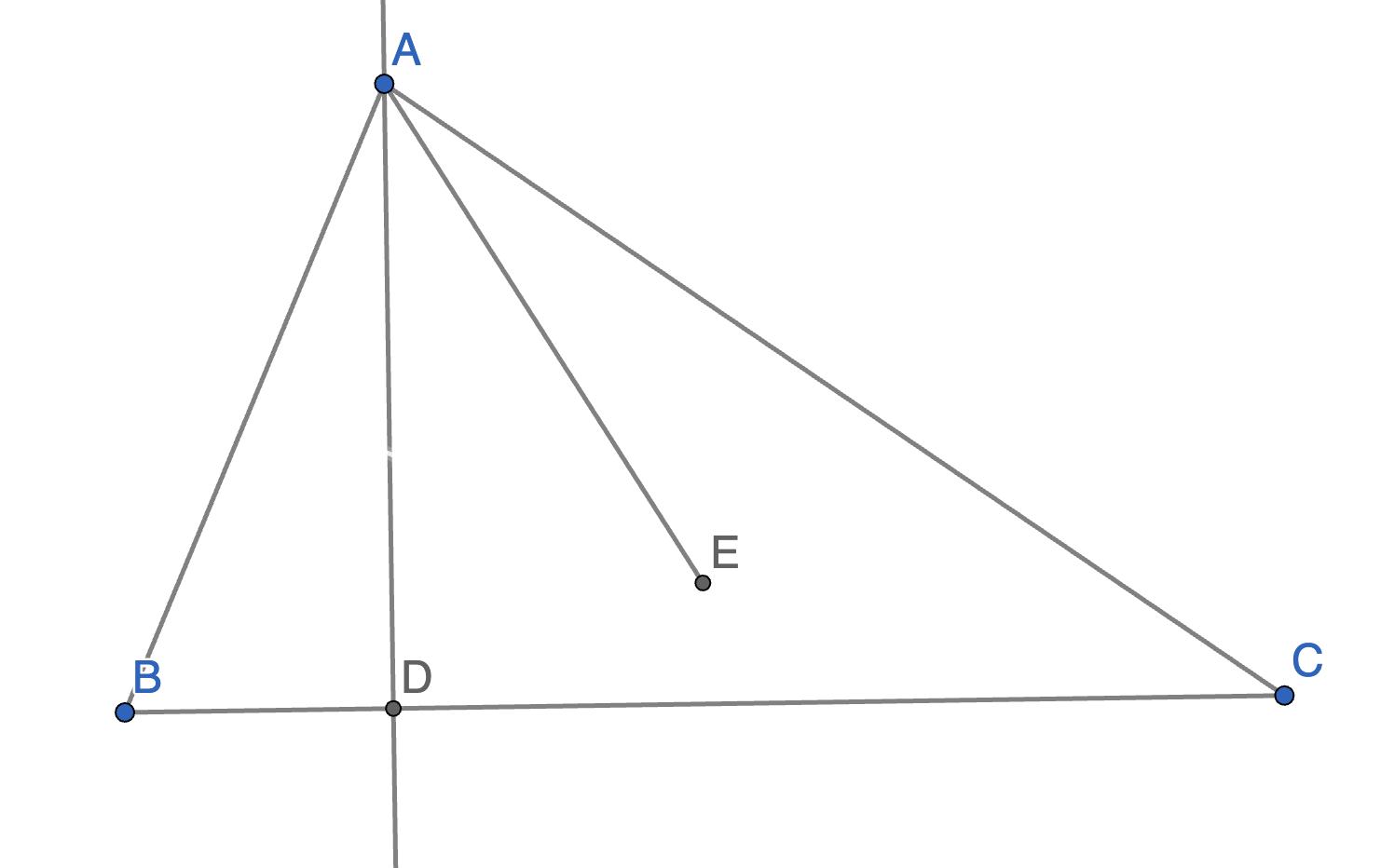
The triangle \(ABC\) is inscribed into the circle with centre \(E\), the line \(AD\) is perpendicular to \(BC\). Prove that the angles \(\angle BAD\) and \(\angle CAE\) are equal.

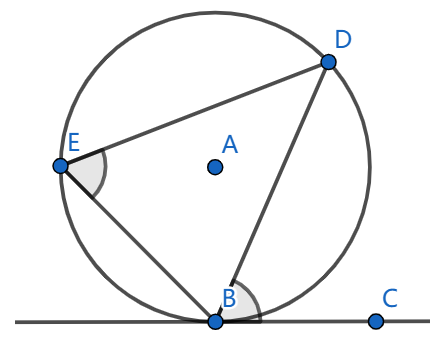
On the diagram below \(BC\) is the tangent line to a circle with the centre \(A\), and it is known that the angle \(\angle ABC = 90^{\circ}\). Prove that the angles \(\angle DEB\) and \(\angle DBC\) are equal.

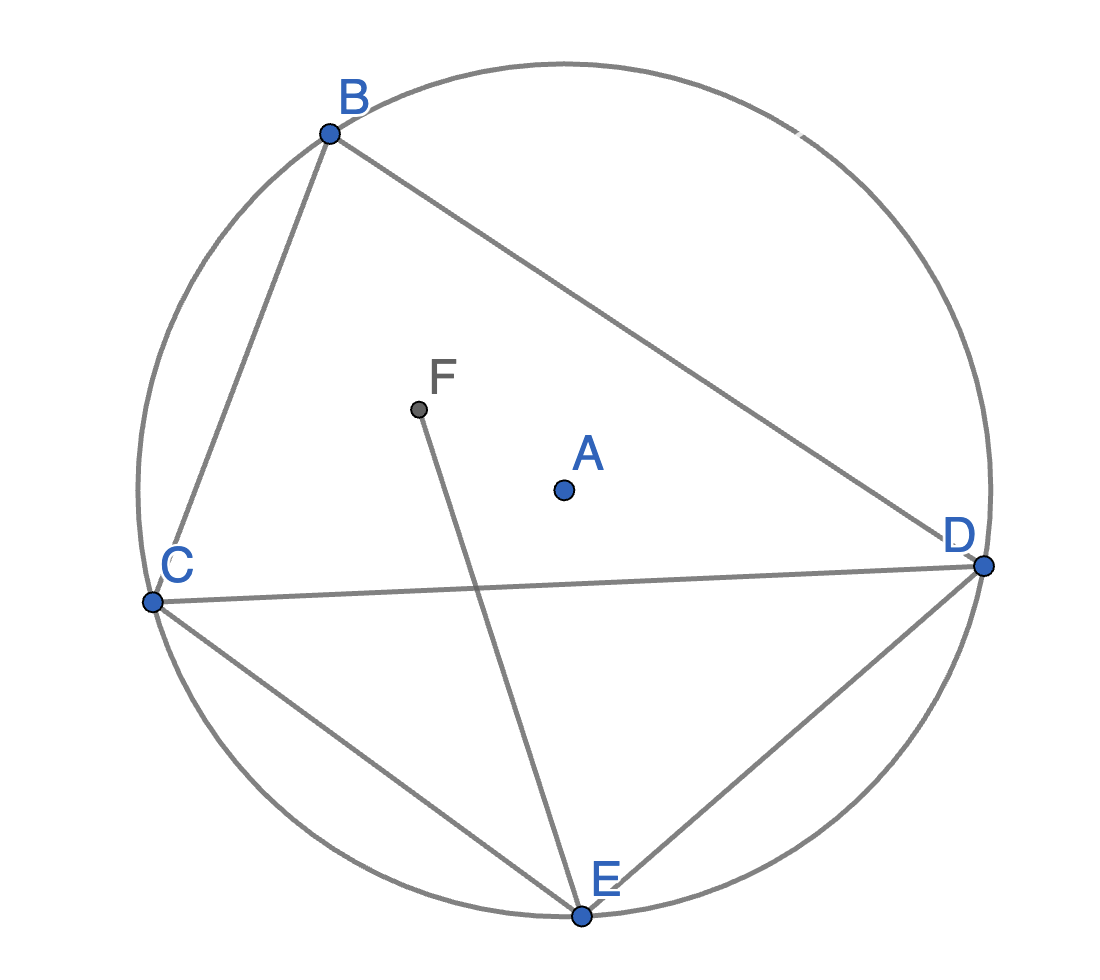
The triangle \(BCD\) is inscribed in a circle with the centre \(A\). The point \(E\) is chosen as the midpoint of the arc \(CD\) which does not contain \(B\), the point \(F\) is the centre of the circle inscribed into \(BCD\). Prove that \(EC = EF = ED\).

Let \(ABC\) and \(DEF\) be such triangles that angles \(\angle ABC = \angle DEF\), \(\angle ACB = \angle DFE\). Prove that the triangles \(ABC\) and \(DEF\) are similar.

The medians \(AD\) and \(BE\) of the triangle \(ABC\) intersect at the point \(F\). Prove that the triangles \(AFB\) and \(DFE\) are similar. What is their similarity coefficient?