Problems

Alice was playing on the \(5\times 5\) lights out board and obtained this light pattern:

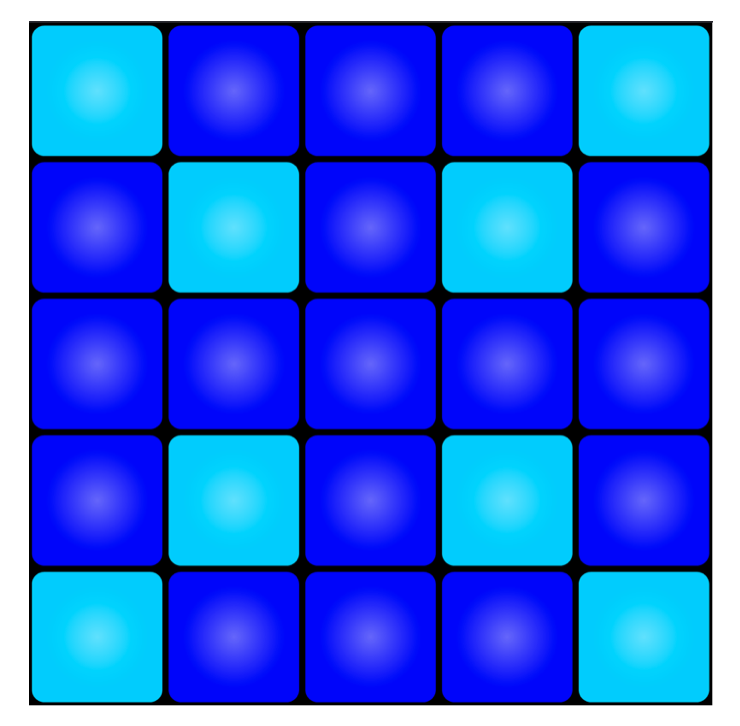
how did she obtain it?

After some playing with the \(3\times 3\) board, Sam guessed that there were \(900\) different light patterns that could be obtained by playing on this board. Was he right?

The original “Lights Out” game works like this: a light pattern is shown on the board, and your task is to turn all the lights off. A light pattern is called solvable if you can complete the game starting from that pattern. Ziheng and Jan are playing on an \(n\times n\) board, and they notice that some patterns are unsolvable. Can you find a rule to decide when a pattern is not solvable?

Long before meeting Snow White, the seven dwarves lived in seven different mines. There is an underground tunnel connecting any two mines. All tunnels were separate, so you could not start in one tunnel and somehow end up in another. Is it possible to walk through every tunnel exactly once without retracing your path?

There is a queue of \(n\) truth tellers and liars. The first person says, “more than half of us are liars". The second person says, “more than a quarter of us are liars". The third person says, “more than an eighth of us are liars", and so on, until the \(n\)th person says, “more than \(\frac{1}{2^n}\) of us are liars". Describe what the number of truth-tellers and liars could be, as well as their placement in the queue. Note that the solutions are not fixed numbers.

There are some coins in a straight line, all showing heads. You can choose any coin to flip. When you flip one, your friend must flip the coins directly next to it (the ones on its left and right, if there are any). For example: if you flip the first coin, your friend only flips the second coin, and if you flip the second coin, your friend flips the first and third coins.

The question is: no matter how many coins there are, can we always make all of them show tails in the end?