Problems
Eleven sages were blindfolded and on everyone’s head a cap of one of \(1000\) colours was put. After that their eyes were untied and everyone could see all the caps except for their own. Then at the same time everyone shows the others one of the two cards – white or black. After that, everyone must simultaneously name the colour of their caps. Will they succeed?
The recertification of the Council of Sages takes place as follows: the king arranges them in a column one by one and puts on a cap of white or black colours for each. All the sages see the colours of all the caps of the sages standing in front, but they do not see the colour of their own and all those standing behind. Once a minute one of the wise men must shout one of the two colours. (each sage shouts out a colour once). After the end of this process the king executes every sage who shouts a colour different from the colour of his cap. On the eve of the recertification all one hundred members of the Council of Sages agreed and figured out how to minimize the number of those executed. How many of them are guaranteed to avoid execution?
At the elections to the High Government every voter who comes, votes for himself (if he is a candidate) and for those candidates who are his friends. The forecast of the media service of the mayor’s office is considered good if it correctly predicts the number of votes at least for one of the candidates, and not considered good otherwise. Prove that for any forecast voters can show up at the elections in such a way that this forecast will not be considered good.
Every even number is not prime. The number \(9\) is not an even number, therefore it is not not prime, i.e: the number \(9\) is prime.
In a school there are three sports clubs, which we call \(A\), \(B\), and \(C\).
A student argues as follows:
“To find how many people attend at least one club, we can add the number of people in each club. However, students who attend all three clubs get counted three times. To fix this, we should subtract them twice. Therefore, the number of people who attend at least one club is \[\text{people in }A+\text{people in }B+\text{people in }C -2\times(\text{people in all three clubs}).\]”
Is this reasoning correct?
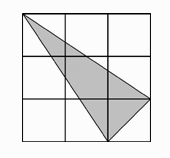
The diagram shows a triangle drawn on a square grid. The area of the shaded triangle is \(9~\text{cm}^2\). What is the area of one of the little squares of the grid?
The first \(2026\) prime numbers are multiplied. How many zeroes are at the end of this resulting number?
Three skiers—Alice, Bob, and Cynthia—compete in a downhill race. They begin skiing in the following order: first Cynthia, then Bob, and finally Alice.
Each skier starts with \(0\) points. Whenever one skier overtakes another during the race, the overtaking skier gains \(1\) point and the skier being overtaken loses \(1\) point.
At the end of the race, Alice crosses the finish line first, and Bob finishes with \(0\) points.
In what position does Cynthia finish?
On the Problemland Space Station, there are \(1000\) tonnes of air, of which \(99\%\) is oxygen. After an unfortunate asteroid impact, some of the air is vented into space. The hull is quickly repaired, and no further loss occurs.
Afterward, measurements reveal that oxygen now makes up only \(98\%\) of the remaining air, and that only oxygen was lost during the incident.
How many tonnes of oxygen remain on the space station?
In the following puzzle, different animals represent different digits, and your goal is to find which digit each animal represents.

Find all possible solutions.