Problems

Is it possible to cut this figure, called "camel"

• a) along the grid lines;

• b) not necessarily along the grid lines;

into \(3\) parts, which you can use to build a square?
(We give you several copies to facilitate drawing)

Cut a square into five triangles in such a way that the area of one of these triangles is equal to the sum of the area of other four triangles.

A circular triangle is a triangle in which the sides are arcs of circles. Below is a circular triangle in which the sides are arcs of circles centered at the vertices opposite to the sides.

Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in the shape of the circular triangle.

Cut this figure into \(4\) identical shapes. (Note: you have to use the entire shape. Rotations and reflections count as identical shapes)

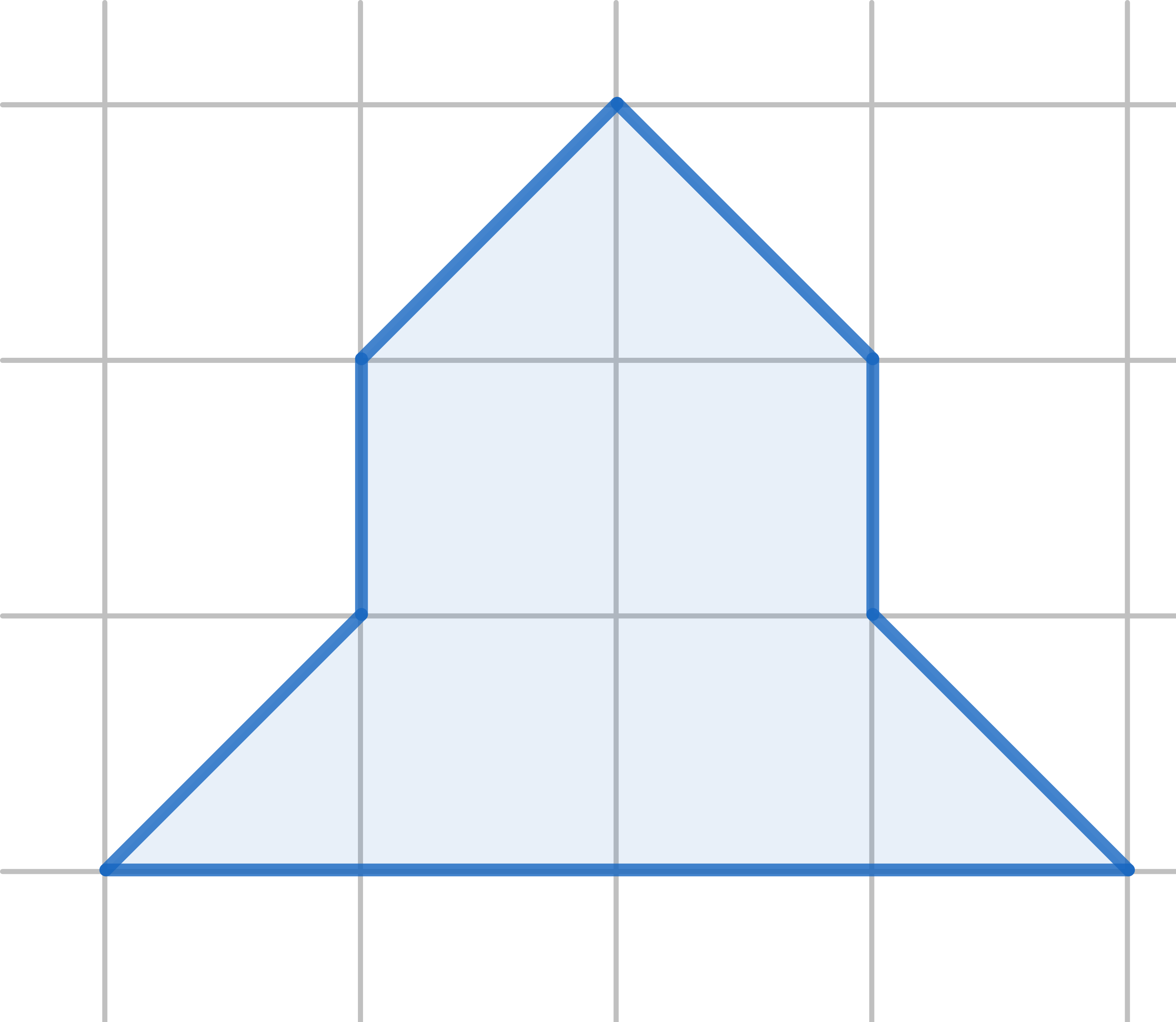
The diagram shows a \(3 \times 3\) square with one corner removed. Cut it into three pieces, not necessarily identical, which can be reassembled to make a square:

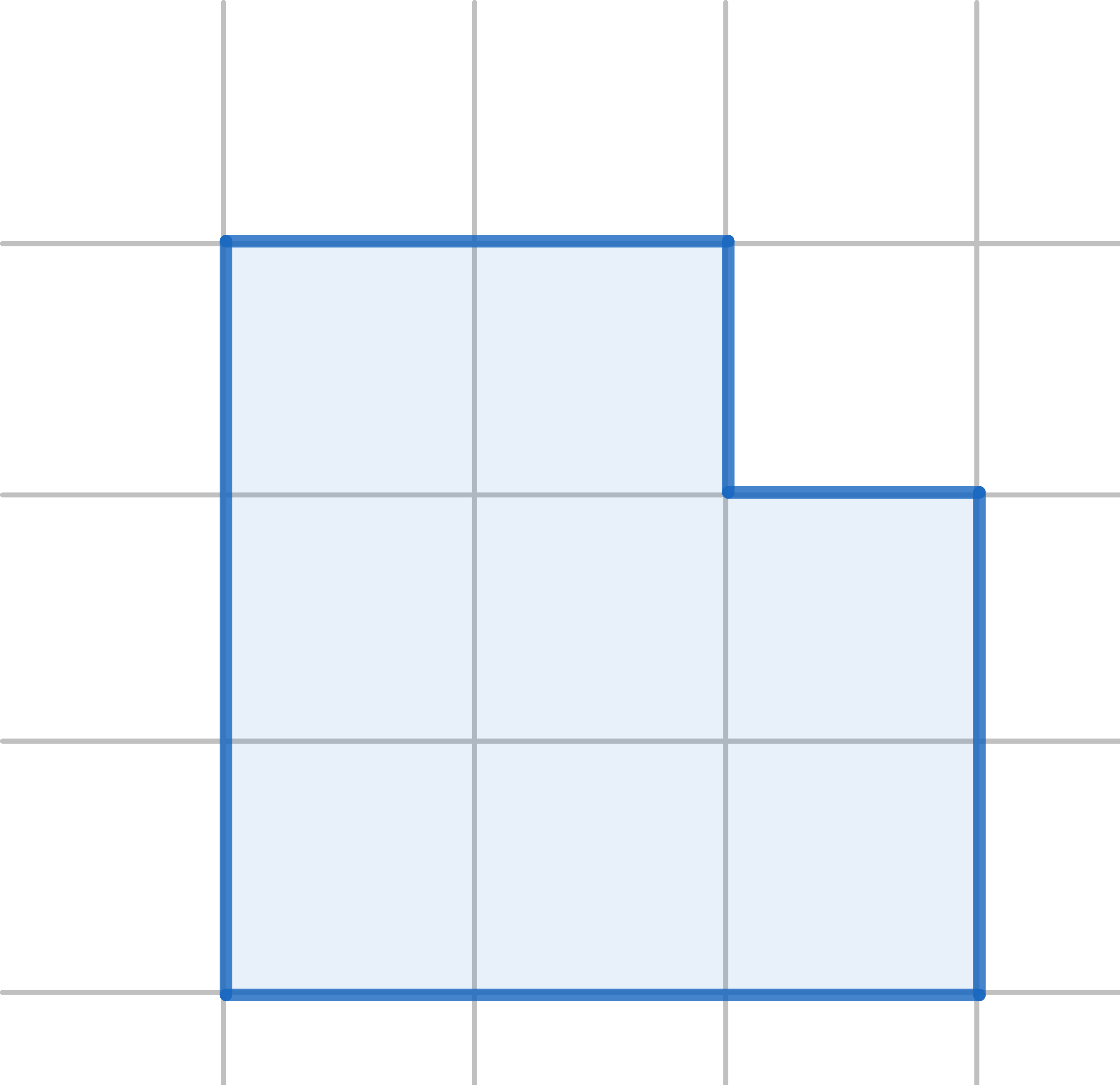
Cut a \(7\times 7\) square into \(9\) rectangles, out of which you can construct any rectangle whose sidelengths are less than \(7\). Show how to construct the rectangles.

Cut a square into three parts and then use these three pieces to form a triangle such that:

1. All its angles are acute (i.e: less than \(90^\circ\)).

2. All its sides are of different lengths.

The Pythagorean Theorem is one of the most important facts about geometry. It says that if we have a right-angled triangle (i.e: it has an angle of \(90^\circ\)), whose longest side measures \(C\), and its other two other sides measure \(A\) and \(B\):

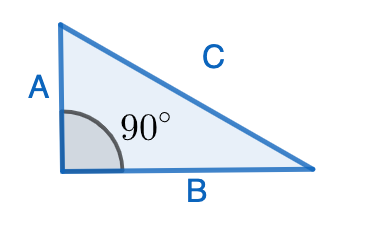
then \(A^2+B^2=C^2\). There are many proofs of this fact, and some involve dissections! Let’s have a look at the following two ways to dissect the same square:

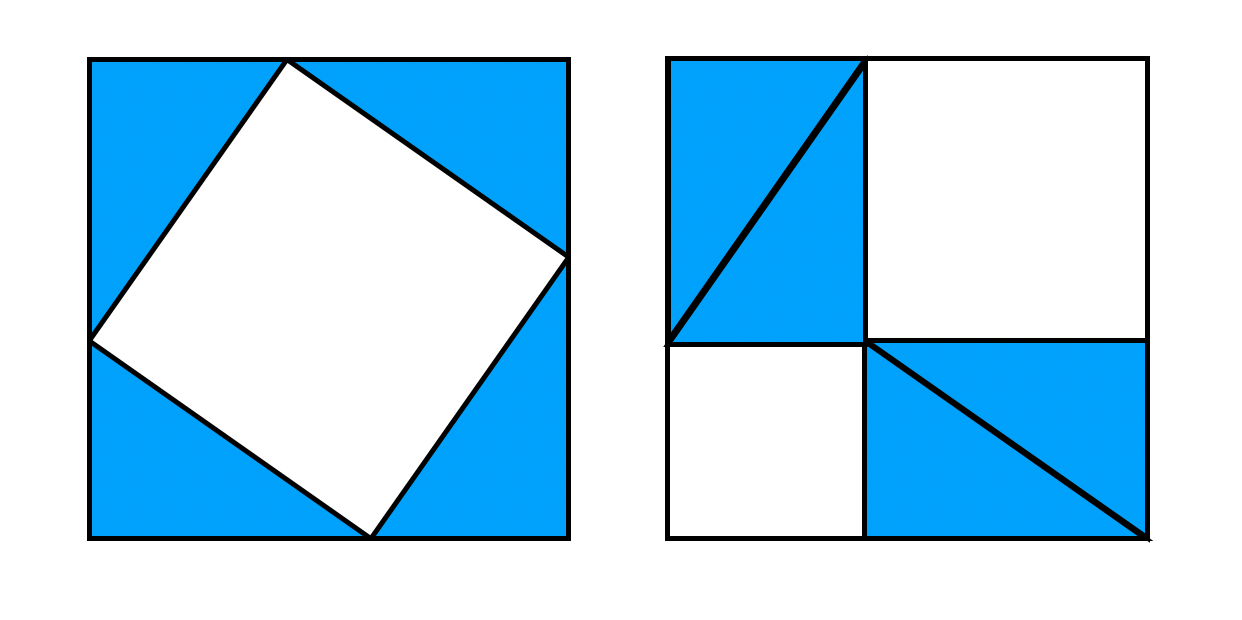
Can you explain how these dissections prove the Pythagorean Theorem?