Problems

Nick writes the numbers \(1,2,\dots,33\), each exactly once, at the vertices of a polygon with \(33\) sides, in some order.

For each side of the polygon, his little sister Hannah writes down the sum of the two numbers at its ends. In total she writes down \(33\) numbers, one for each side.

It turns out that when read in order around the polygon, these \(33\) sums are \(33\) consecutive whole numbers.

Can you find an arrangement of the numbers written by Nick that makes this happen?

Is it possible to arrange the numbers \(1,\, 2,\, ...,\, 50\) at the vertices and middles of the sides of a regular \(25\)-gon so that the sum of the three numbers at the ends and in the middle of each side is the same for all sides?

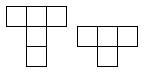
Draw a shape that can both be cut into 4 copies of the figure on the left or alternatively into 5 copies of the figure on the right. (the figures can be rotated).