Problems
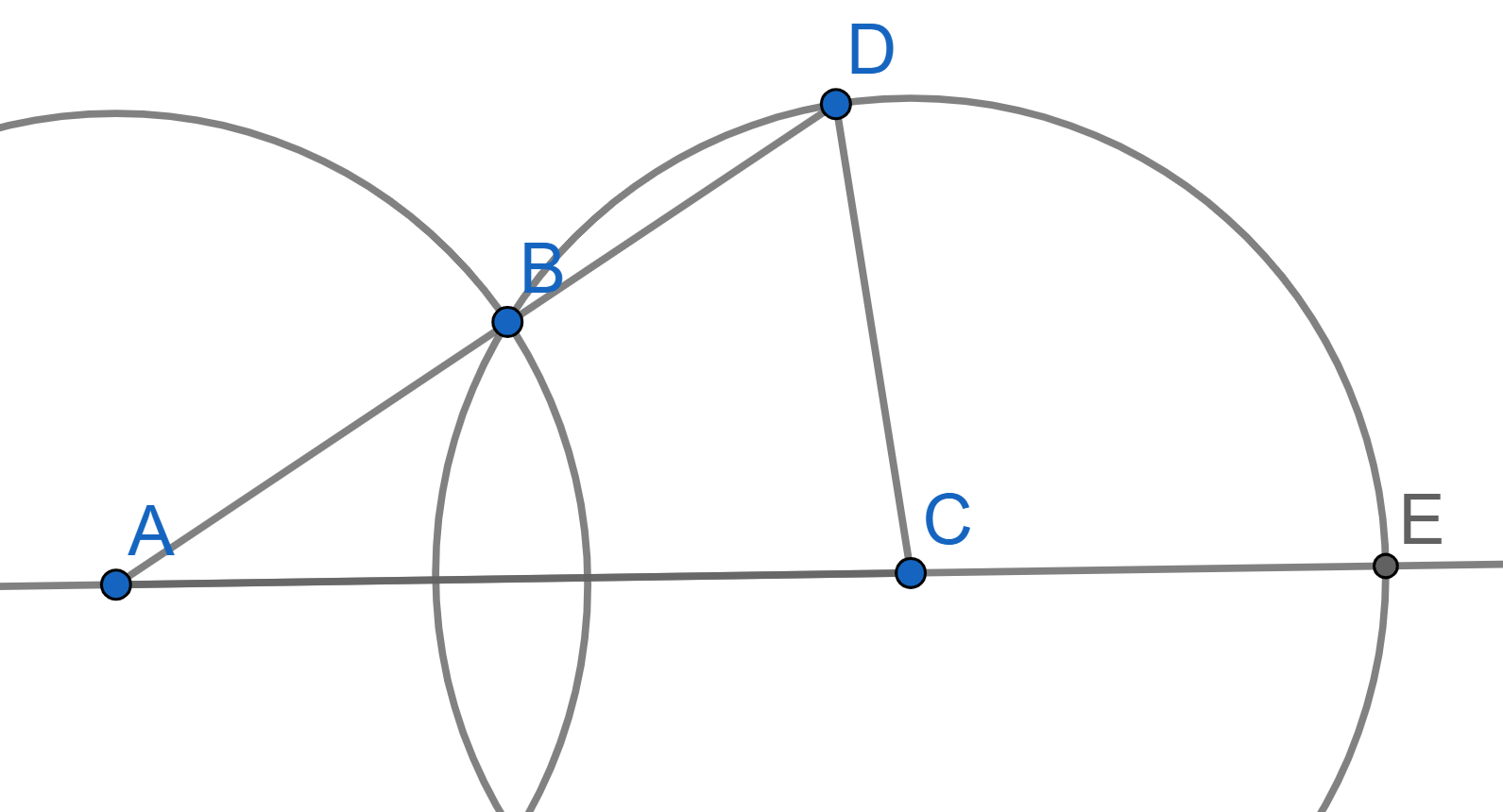
Two intersecting circles of radius \(R\) are given, and the distance between their centers is greater than \(R\). Prove that \(\angle ECD = 3\angle CAD\).
Find all triangles in which the angles form an arithmetic progression, and the sides form: a) an arithmetic progression; b) a geometric progression.
Prove that the point \(X\) lies on the line \(AB\) if and only if \(\overrightarrow{OX} = t \overrightarrow{OA} + (1 - t) \overrightarrow{OB}\) for some \(t\) and any point \(O\).
Several points are given and for some pairs \((A, B)\) of these points the vectors \(\overrightarrow{AB}\) are taken, and at each point the same number of vectors begin and end. Prove that the sum of all the chosen vectors is \(\vec{0}\).
Prove that the medians of the triangle \(ABC\) intersect at one point and that point divides the medians in a ratio of \(2: 1\), counting from the vertex.
Prove that, when a circle is translated it becomes a circle.
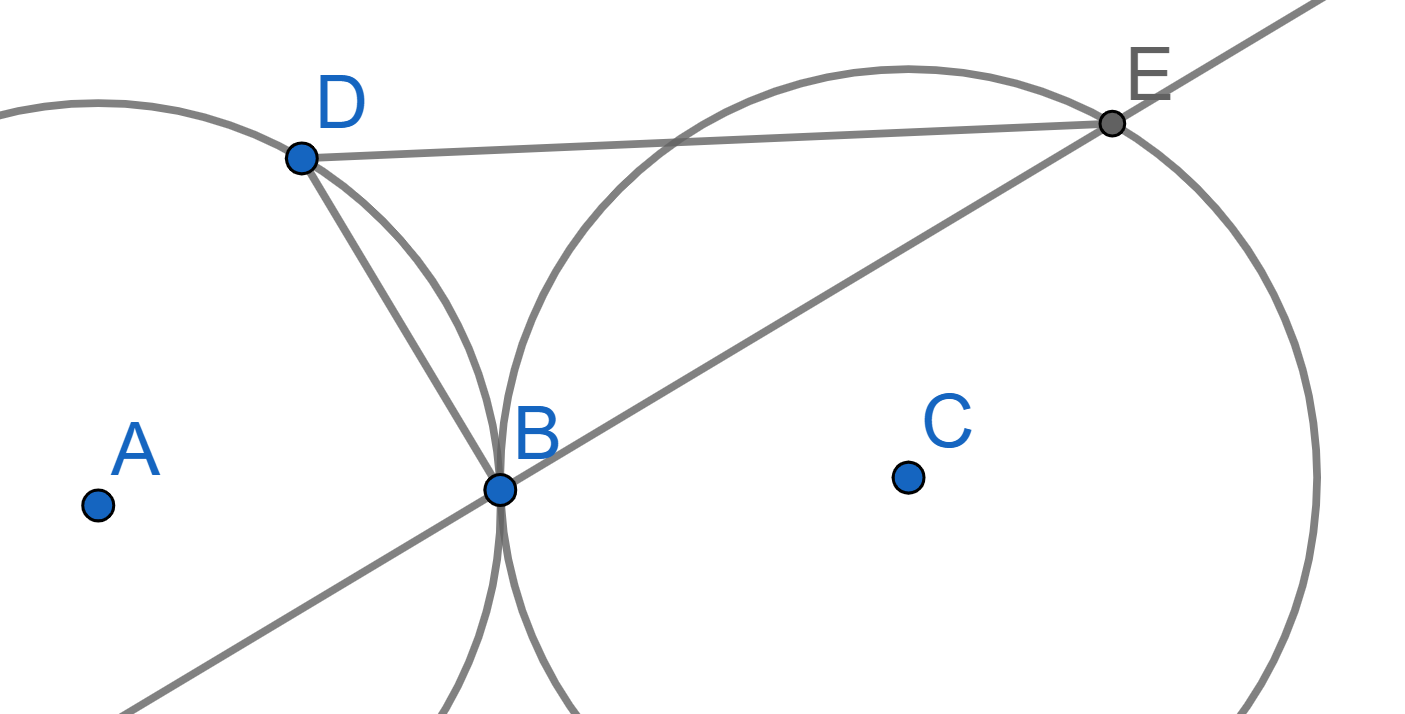
Two circles of radius \(R\) touch at point \(B\). On one of them, point \(D\) is chosen and on the other point \(E\) is chosen. These points have a property of \(\angle DBE = 90^{\circ}\). Prove that \(DE = 2R\).
Two circles of radius \(R\) intersect at points \(B\) and \(D\). Consider the perpendicular bisector of the segment \(BD\). This line meets the two circles again at points \(F\) and \(G\), both chosen on the same side of \(BD\). Prove that \[BD^2 + FG^2 = 4R^2.\]
Inside the rectangle \(ABCD\), the point \(E\) is taken. Prove that there exists a convex quadrilateral with perpendicular diagonals of lengths \(AB\) and \(BC\) whose sides are equal to \(AE\), \(BE\), \(CE\), \(DE\).
Prove that, with central symmetry, a circle transforms into a circle.