Problems

Solve the puzzle: \[\textrm{AC}\times\textrm{CC}\times\textrm{K} = 2002.\] Different letters correspond to different digits, identical letters correspond to identical digits.

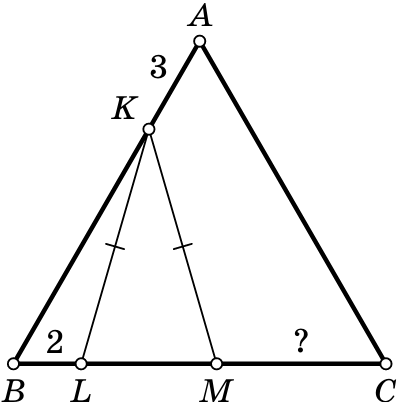
The triangle \(ABC\) is equilateral. The point \(K\) is chosen on the side \(AB\) and points \(L\) and \(M\) are on the side \(BC\) in such a way that \(L\) lies on the segment \(BM\). We have the following properties: \(KL = KM,\) \(BL = 2,\, AK = 3.\) Find the length of \(CM\).

• We call two figures congruent if their corresponding sides and angles are equal. Let \(ABD\) an \(A'B'D'\) be two right-angled triangles with right angle \(D\). Then if \(AD=A'D'\) and \(AB=A'B'\) then the triangles \(ABD\) and \(A'B'D'\) are congruent.

• It follows from the previous statement that if two lines \(AB\) and \(CD\) are parallel than angles \(BCD\) and \(CBA\) are equal.

We prove the other two assertions from the description:

• The sum of all internal angles of a triangle is also \(180^{\circ}\).

• In an isosceles triangle (which has two sides of equal lengths), two angles touching the third side are equal.

In the triangle \(ABC\) the sides are compared as following: \(AC>BC>AB\). Prove that the angles are compared as follows: \(\angle B > \angle A > \angle C\).

Consider a quadrilateral \(ABCD\). Choose a point \(E\) on side \(AB\). A line parallel to the diagonal \(AC\) is drawn through \(E\) and meets \(BC\) at \(F\). Then a line parallel to the other diagonal \(BD\) is drawn through \(F\) and meets \(CD\) at \(G\). And then a line parallel to the first diagonal \(AC\) is drawn through \(G\) and meets \(DA\) at \(H\). Prove the \(EH\) is parallel to the diagonal \(BD\).

Find all solutions of the puzzle \(HE \times HE = SHE\). Different letters denote different digits, while the same letters correspond to the same digits.

Cut an arbitrary triangle into parts that can be used to build a triangle that is symmetrical to the original triangle with respect to some straight line (the pieces cannot be inverted, they can only be rotated on the plane).

The numbers from \(1\) to \(9\) are written in a row. Is it possible to write down the same numbers from \(1\) to \(9\) in a second row beneath the first row so that the sum of the two numbers in each column is an exact square?

On a Halloween night ten children with candy were standing in a row. In total, the girls and boys had equal amounts of candy. Each child gave one candy to each person on their right. After that, the girls had \(25\) more candy than they used to. How many girls are there in the row?