Problems

Cut a \(7\times 7\) square into \(9\) rectangles, out of which you can construct any rectangle whose sidelengths are less than \(7\). Show how to construct the rectangles.

There are \(16\) cities in the kingdom. Prove that it is not possible to build a system of roads in such a way that one can get from any city to any other without passing through more than one city on the way, and with at most four roads coming out of each city.

There are \(16\) cities in the kingdom. Prove that it is possible to build a system of roads in such a way that one can get from any city to any other without passing through more than one city on the way, and with at most five roads coming out of each city.

Recall that a line is tangent to a circle if they have only one point of intersection, a circle is called inscribed in a polygon if it is tangent to every side as a segment of that polygon.
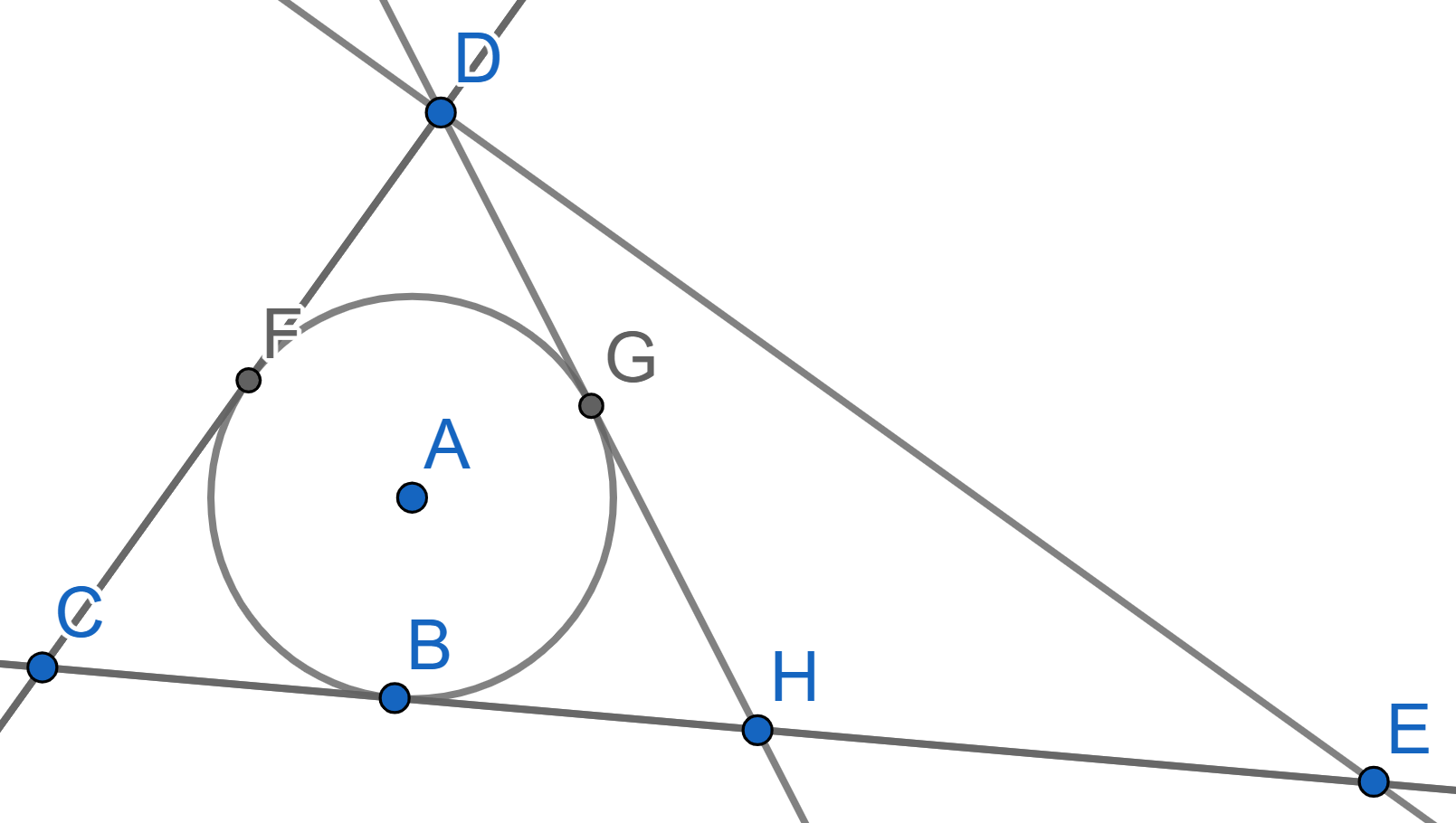
In the triangle \(CDE\) the angle \(\angle CDE = 90^{\circ}\) and the line \(DH\) is the median. A circle with center \(A\) is inscribed in the triangle \(CDH\) and is tangent to the segment \(DH\) in its middle, let’s denote it as \(G\), so \(GH=DG\). Find the angles of the triangle \(CDE\).

Recall that a line is tangent to a circle if they have only one point of intersection, a circle is called inscribed in a polygon if it is tangent to every side as a segment of that polygon.
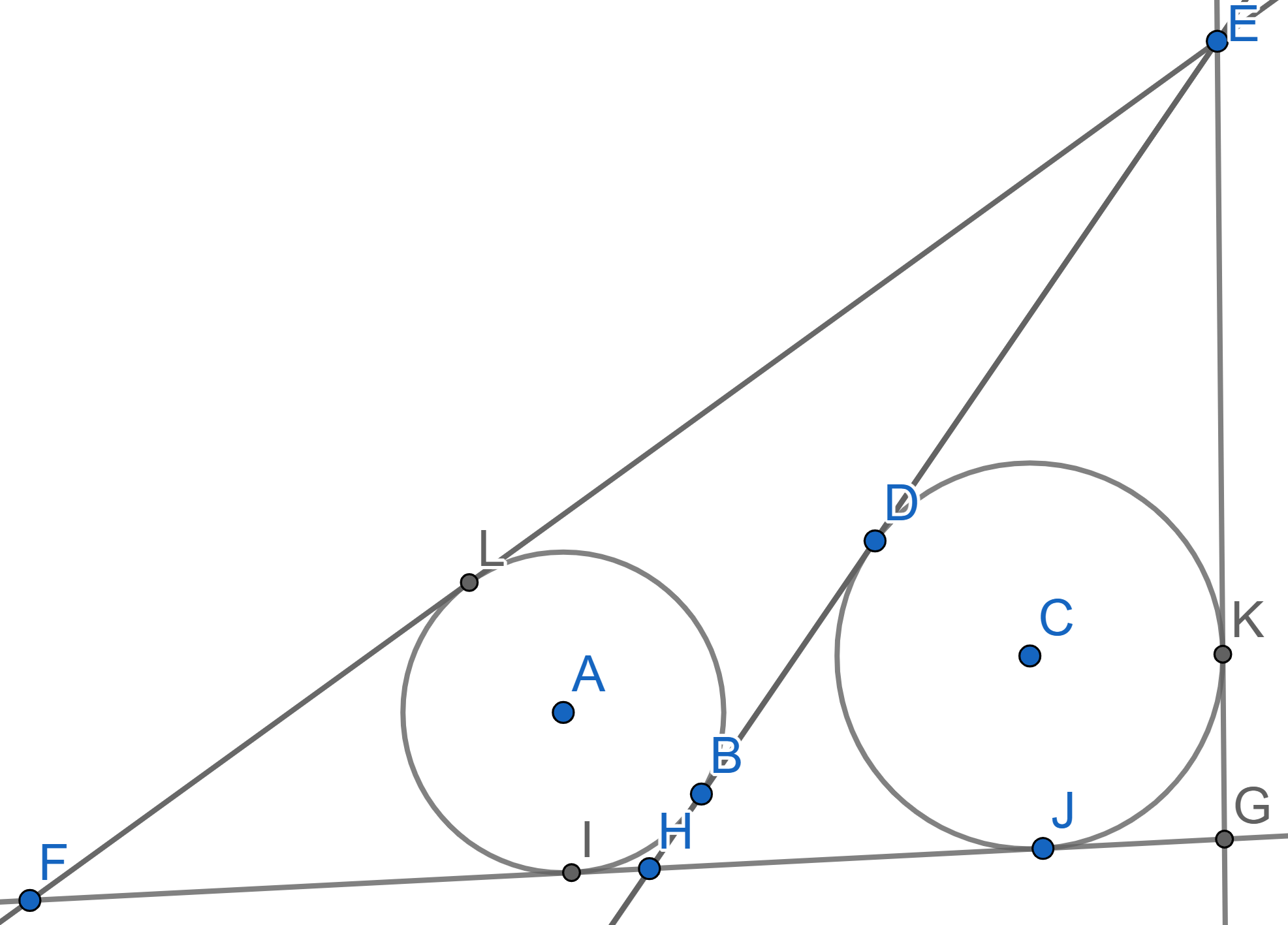
In the triangle \(EFG\) the line \(EH\) is the median. Two circles with centres \(A\) and \(C\) are inscribed into triangles \(EFH\) and \(EGH\) respectively, they are tangent to the median \(EH\) at the points \(B\) and \(D\). Find the length of \(BD\) if \(EF-EG=2\).

Is it possible to cover a \(6 \times 6\) board with the \(L\)-tetraminos without overlapping? The pieces can be flipped and turned.

Is it possible to cover a \((4n+2) \times (4n+2)\) board with the \(L\)-tetraminos without overlapping for any \(n\)? The pieces can be flipped and turned.

Is it possible to cover a \(4n \times 4n\) board with the \(L\)-tetraminos without overlapping for any \(n\)? The pieces can be flipped and turned.

There are \(100\) people standing in line, and one of them is Arthur. Everyone in the line is either a knight, who always tells the truth, or a liar who always lies. Everyone except Arthur said, "There are exactly two liars between Arthur and me." How many liars are there in this line, if it is known that Arthur is a knight?

Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in the shape of a square, or slightly harder in a shape of a given rectangle.