Problems

The prime factorization of the number \(b\) is \(2 \times 5^2 \times 7 \times 13^2 \times 17\). The prime factorization of the number \(c\) is \(2^2 \times 5 \times 7^2 \times 13\). Is the first number divisible by the second one? Is the product of these two numbers, \(b \times c\), divisible by \(49000\)?

Find all the prime numbers \(p\) such that there exist natural numbers \(x\) and \(y\) for which \(p^x = y^3 + 1\).

Determine all prime numbers \(p\) such that \(5p+1\) is also prime.

Find all natural numbers \(n\) for which there exist integers \(a,b,c\) such that \(a+b+c = 0\) and the number \(a^n + b^n + c^n\) is prime.

Find all the prime numbers \(p\) such that the number \(2p^2+1\) is also prime.

A graph is called Bipartite if it is possible to split all its vertices into two groups in such a way that there are no edges connecting vertices from the same group. Find out whic of the following graphs are bipartite and which are not:

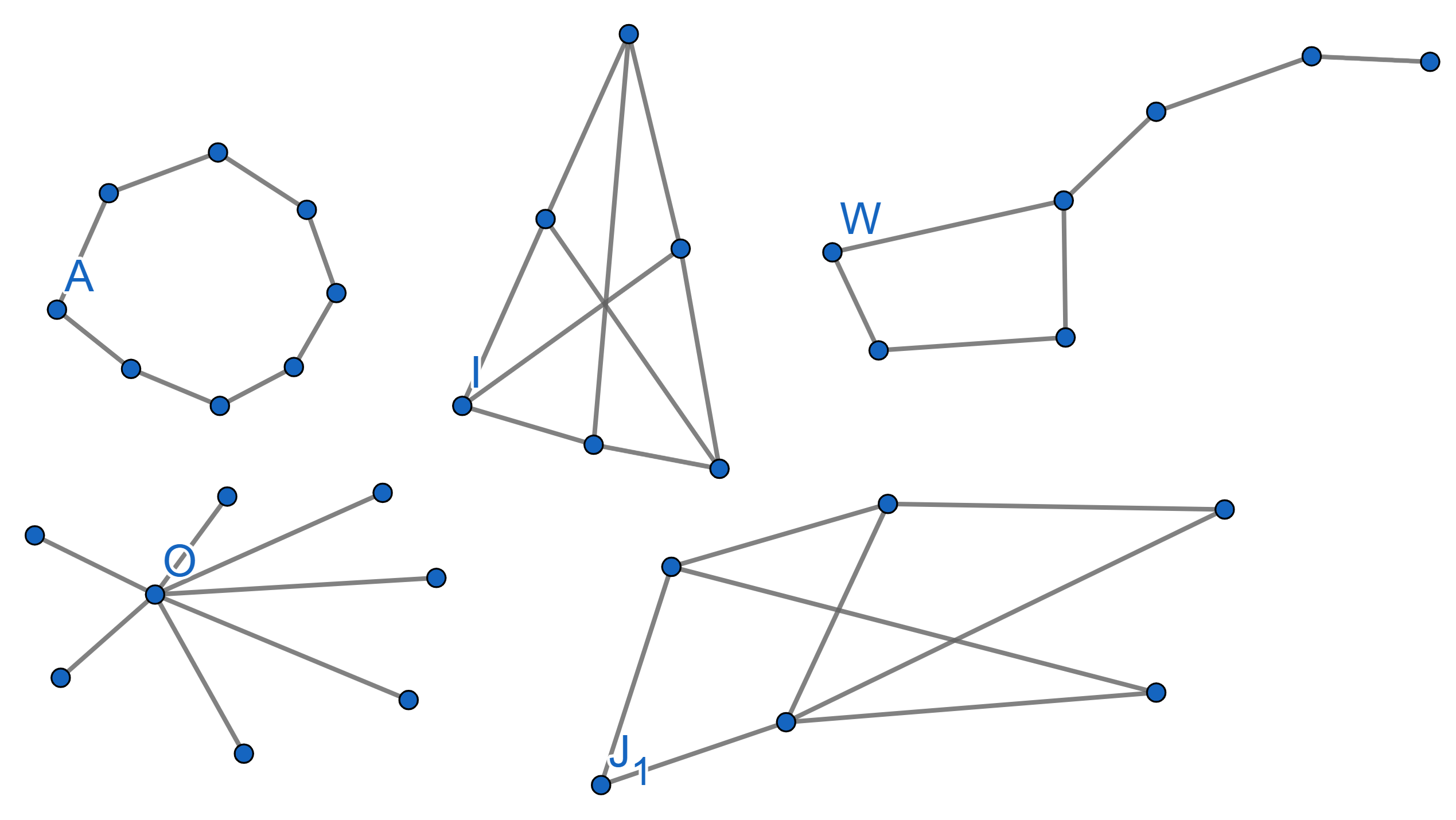
Show that a bipartite graph with \(n\) vertices cannot have more than \(\frac{n^2}{4}\) edges.

In a graph \(G\), we call a matching any choice of edges in \(G\) in such a way that all vertices have only one edge among chosen connected to them. A perfect matching is a matching which is arranged on all vertices of the graph.
Let \(G\) be a graph with \(2n\) vertices and all the vertices have degree at least \(n\) (the number of edges exiting the vertex). Prove that one can choose a perfect matching in \(G\).

A new customer comes to the hotel and wants a room. It happened today that all the rooms are occupied. What should you do?

Now imagine you got \(10\) new guests arriving to the completely full hotel. What should you do now?