Problems
Suppose you have a coffee mug made of stretchy and expandable material. How do you mold it into a donut that has a hole inside?
Take a straight string of finite length. Put the right half on top of the left half to form a hoop, and then pass it (the piece now on top) through the hoop from underneath. Glue the two ends together to form the trefoil knot.
Draw a sequence of pictures to illustrate the formation of the trefoil knot.
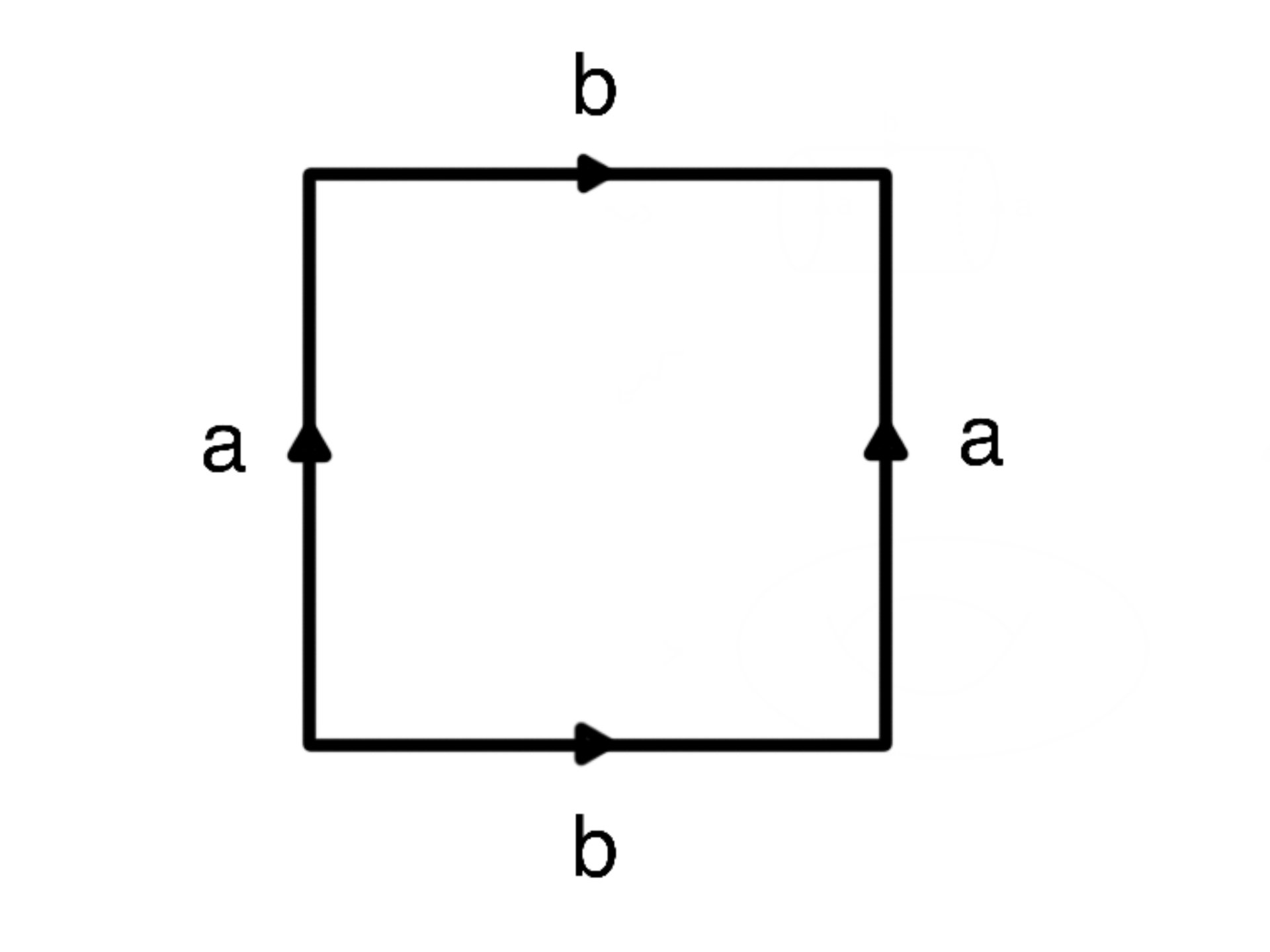
In the picture below, each side is glued in the same direction as its opposite side. Draw a sequence of pictures to show the gluing process and the final shape.
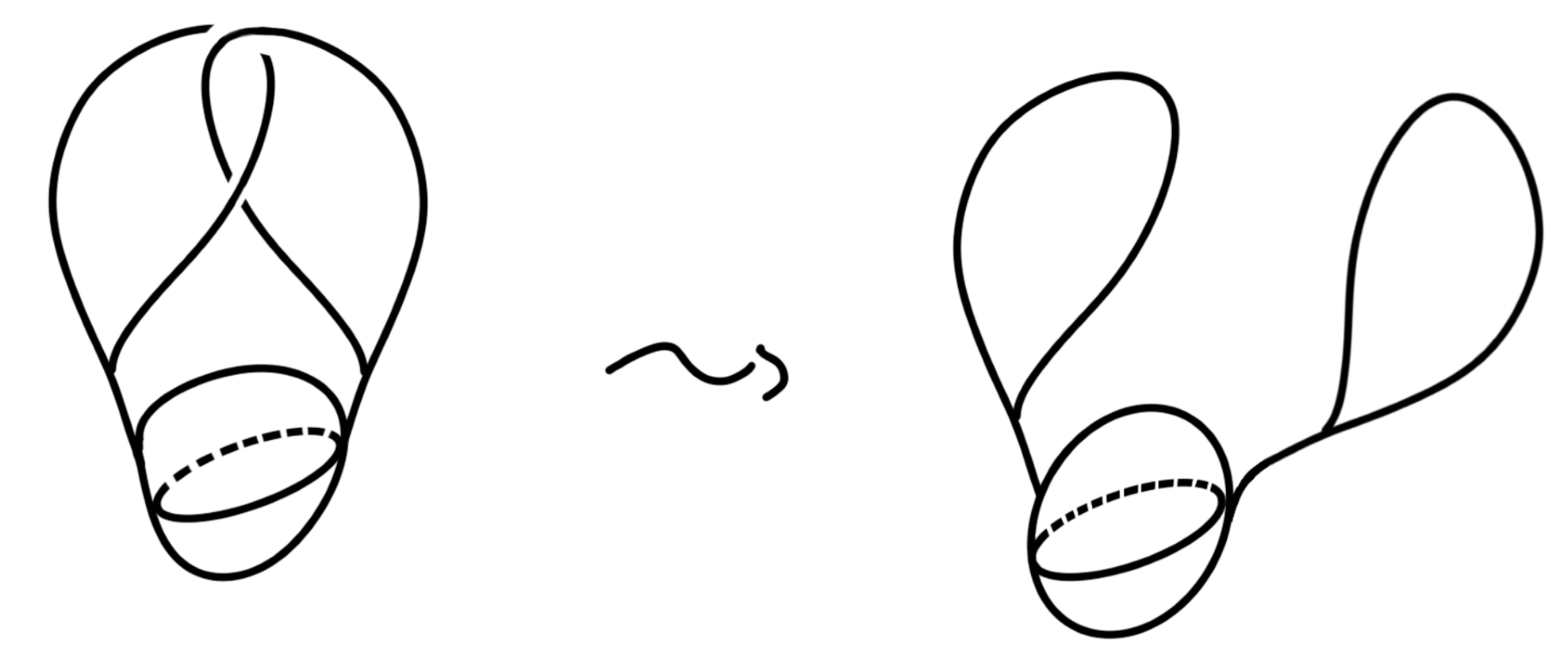
Take a straight string of finite length. Wrap the right half over and then under the left half so that it is pointing to the right again and there is a hoop. Pass the right pointing piece through the hoop from above. Glue the two ends together to form the figure-8 knot.
Draw a sequence of pictures to illustrate the formation of the figure-8 knot, seen below.

Explain why it is possible to have a picture of a figure-8 knot with 100 crossings.
Imagine the Earth is a perfectly round solid ball. Let us drill from the North Pole, London and Beijing simultaneously and meet at the centre of Earth. A ball with three openings is formed. The surface of this ball is shown on the left of the picture below. Describe how to stretch this surface so that it looks like the surface of a donut with two holes as shown on the right.
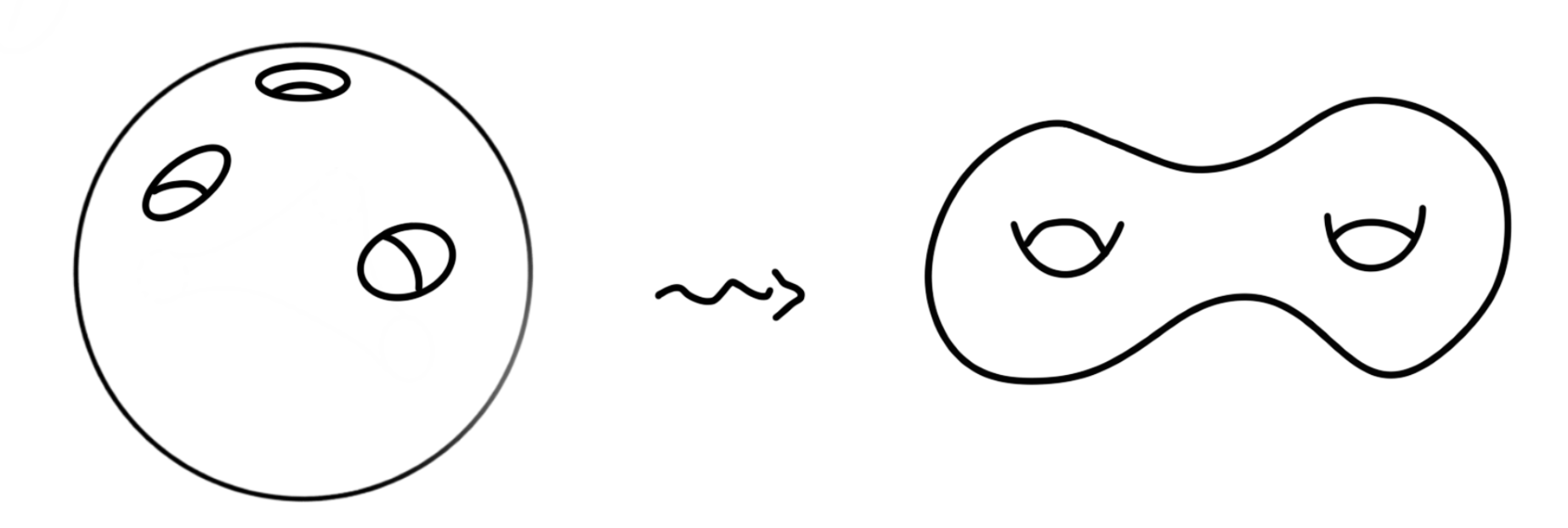
The unknot is the simplest knot, formed by taking a piece of straight string and gluing its two ends together. In reality, there is no knot! Now, which of the following two knots is the unknot?
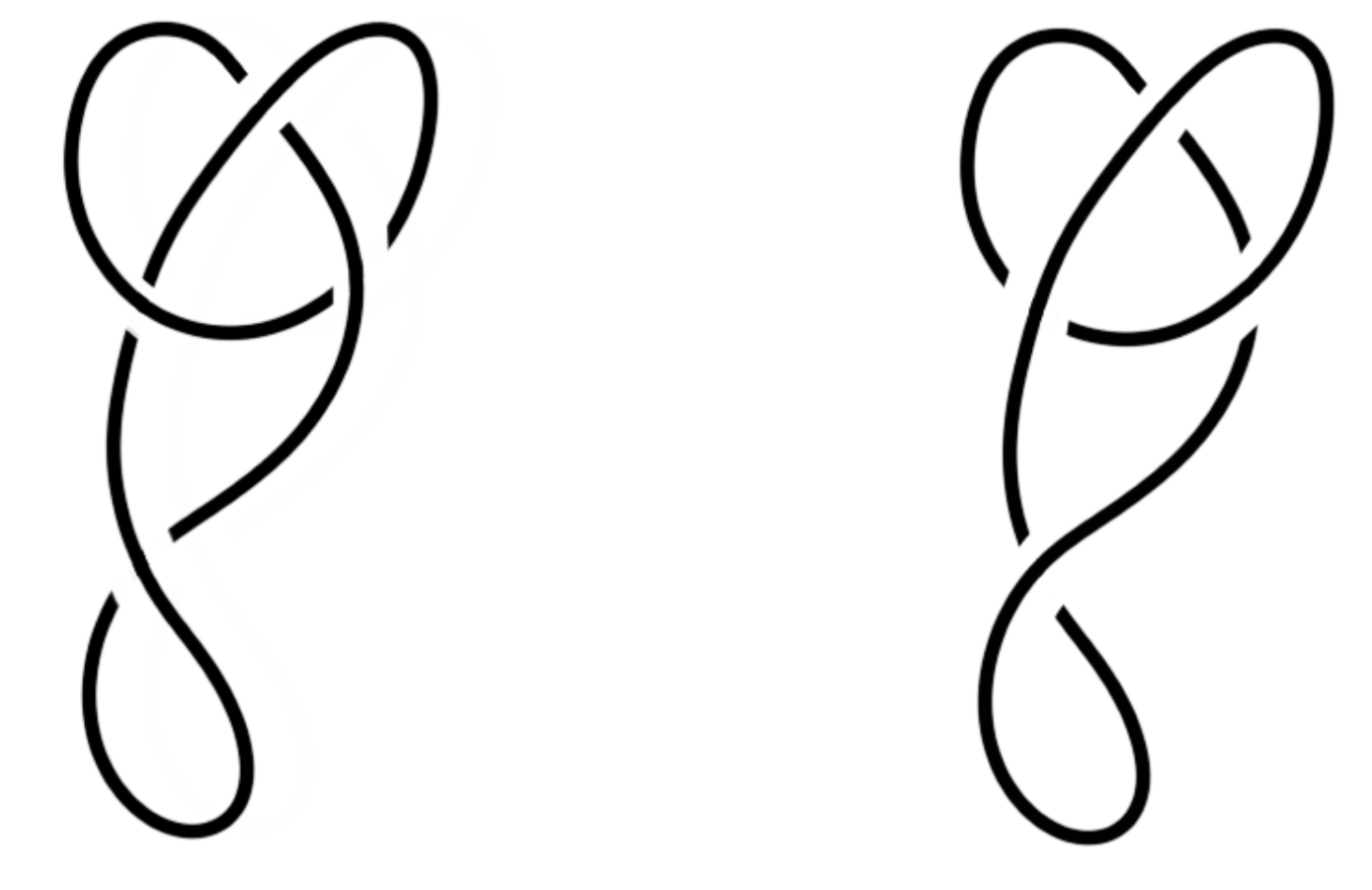
Show that a knot that can be drawn with only one crossing must be the unknot.
How do you go from the left figure to the right one without cutting, tearing or passing the strings through each other? The blue object consist of two circles glued together at a point.
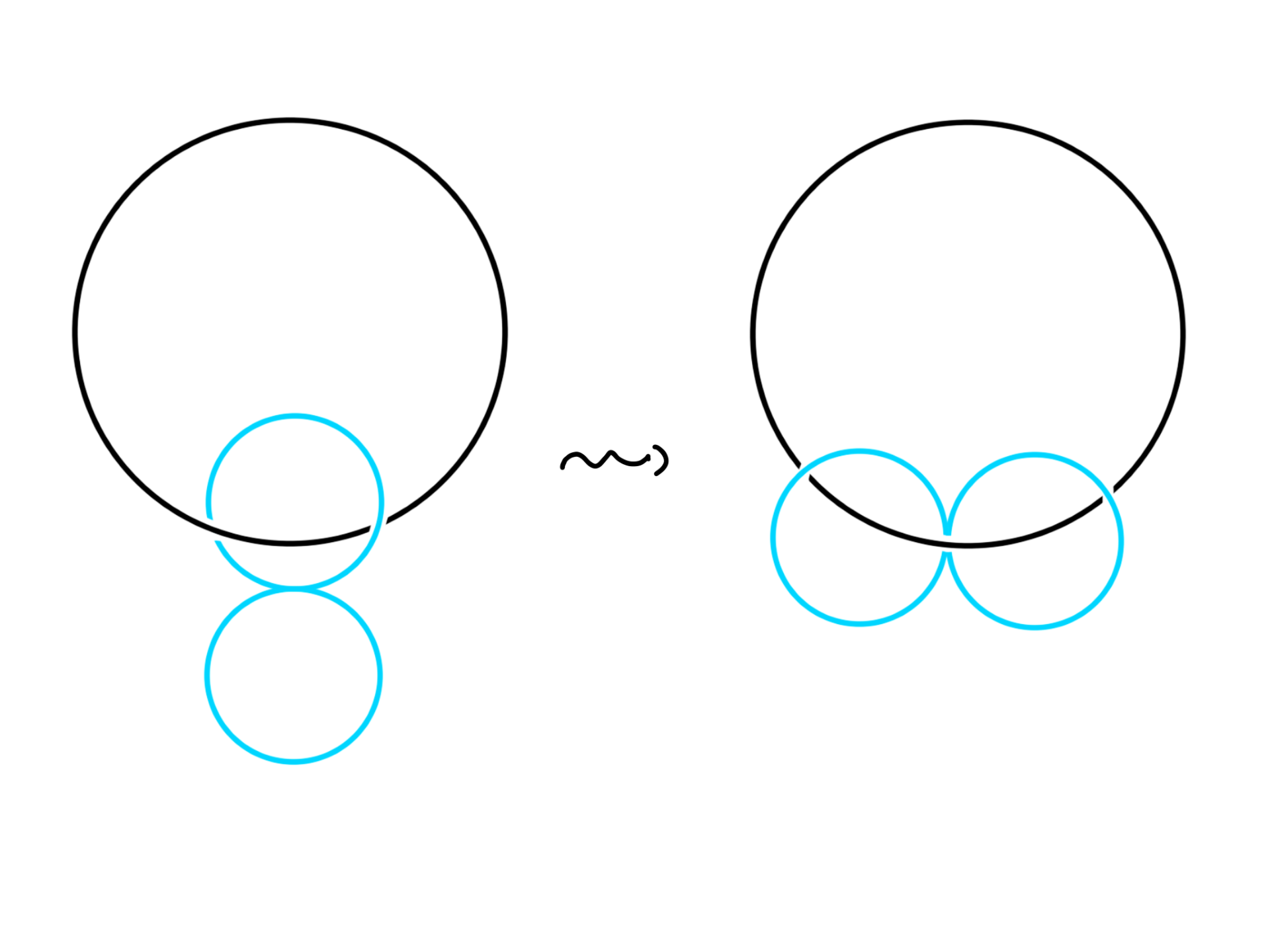
The left figure is formed by two interlocking loops joined to a solid ball. The right figure is formed by two unlinked loops joined to a solid ball. Describe how to transform the left into the right without cutting, tearing or passing the loops through each other.
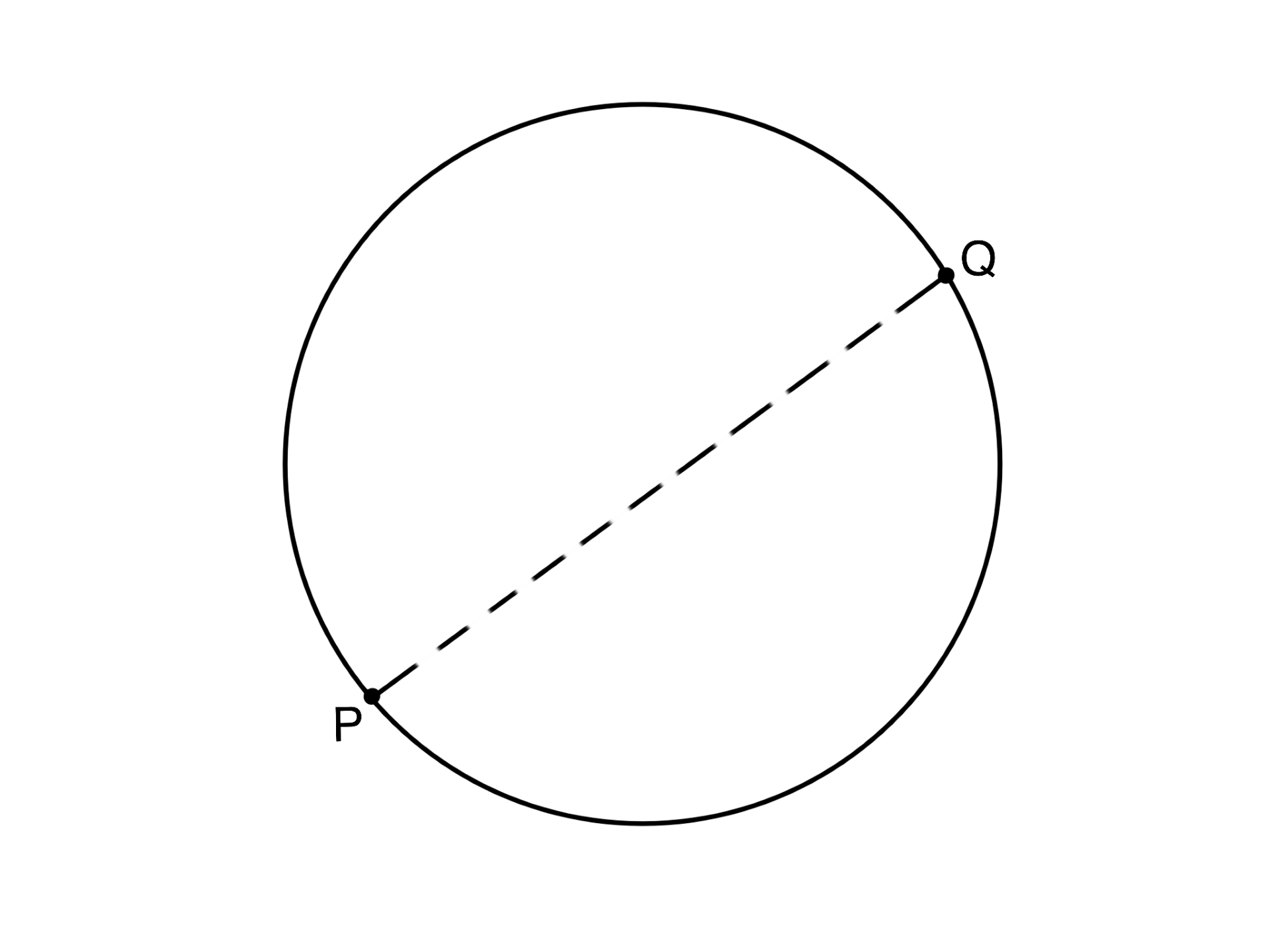
A pair of points on a circle are said to be antipodal if they are on two opposite ends of a common diameter. P and Q in the picture are antipodal points. If we glue every pair of antipodal points on a circle, then what is the resulting shape?