Problems

Prove that the product of five consecutive integers is divisible by \(120\).

Prove that the vertices of a planar graph can be coloured in (at most) six different colours such that every pair of vertices joined by an edge are of different colours.

Note: a graph is planar if it can be drawn in the plane with no edges crossing. For example, three houses, each of which is connected to three utilities, is not a planar graph.
You may find it useful to use the Euler characteristic: a planar graph with \(v\) vertices, \(e\) edges and \(f\) faces satisfies \(v-e+f=2\).

Norman painted the plane using two colours: red and yellow. Both colours are used at least once. Show that no matter how Norman does this, there is a red point and a yellow point exactly \(1\)cm apart.

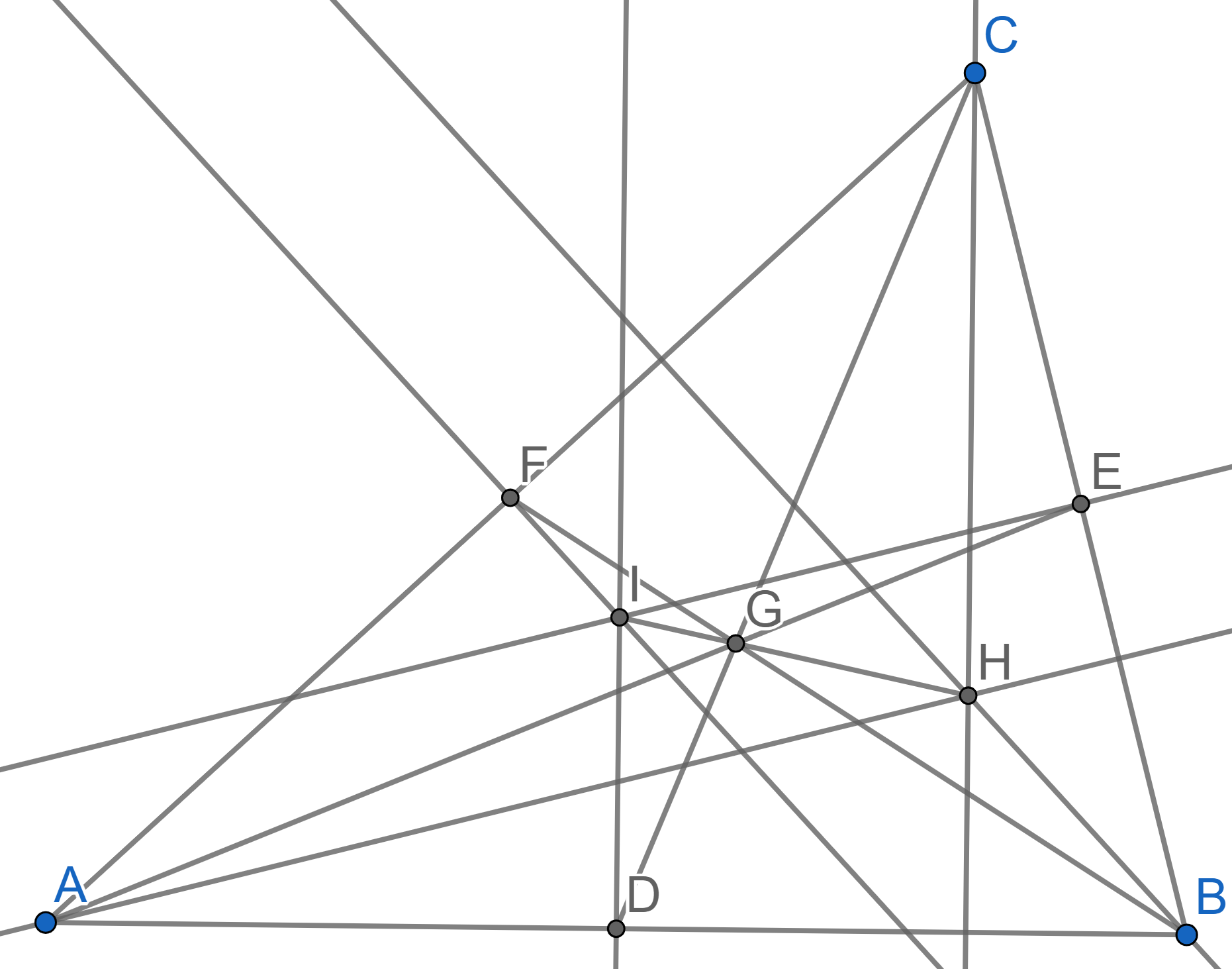
Let \(ABC\) be a non-isosceles triangle. The point \(G\) is the point of intersection of the medians \(AE\), \(BF\), \(CD\), the point \(H\) is the point of intersection of all heights, the point \(I\) is the center of the circumscribed circle for \(ABC\), or the point of intersection of all perpendicular bisectors to the segments \(AB\), \(BC\), \(AC\).
Prove that points \(I,G,H\) lie on one line and the ratio \(IG:GH = 1:2\).

Paloma wrote digits from \(0\) to \(9\) in each of the \(9\) dots below, using each digit at most once. Since there are \(9\) dots and \(10\) digits, she must have missed one digit.

In the triangles, Paloma started writing either the three digits at the corners added together (the sum), or the three digits at the corners multiplied together (the product). She gave up before finishing the final two triangles.

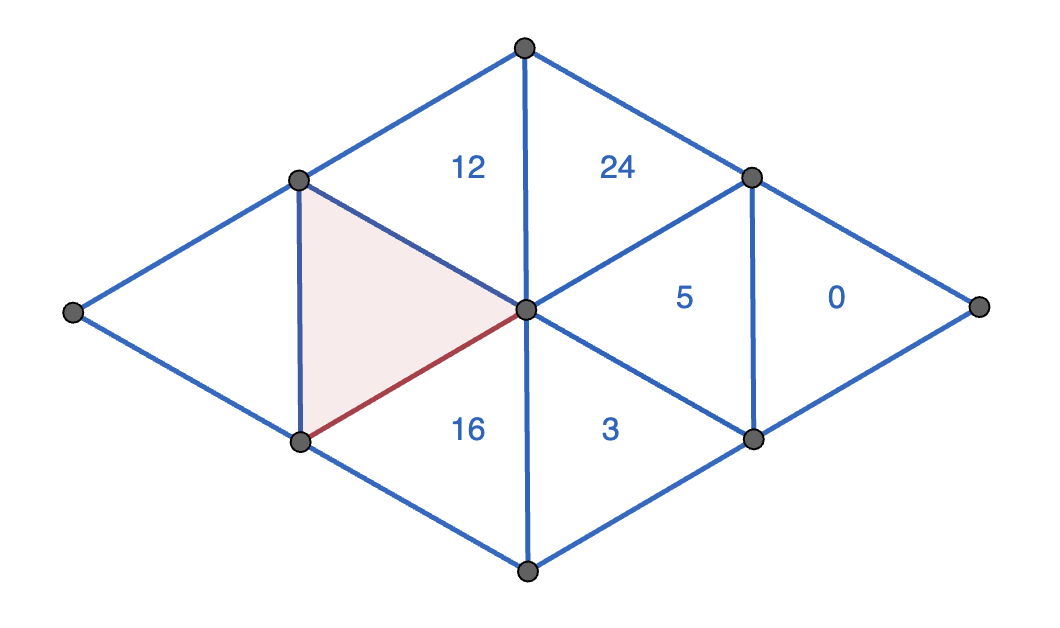
What numbers could Paloma have written in the interior of the red triangle? Demonstrate that you’ve found all of the possibilities.

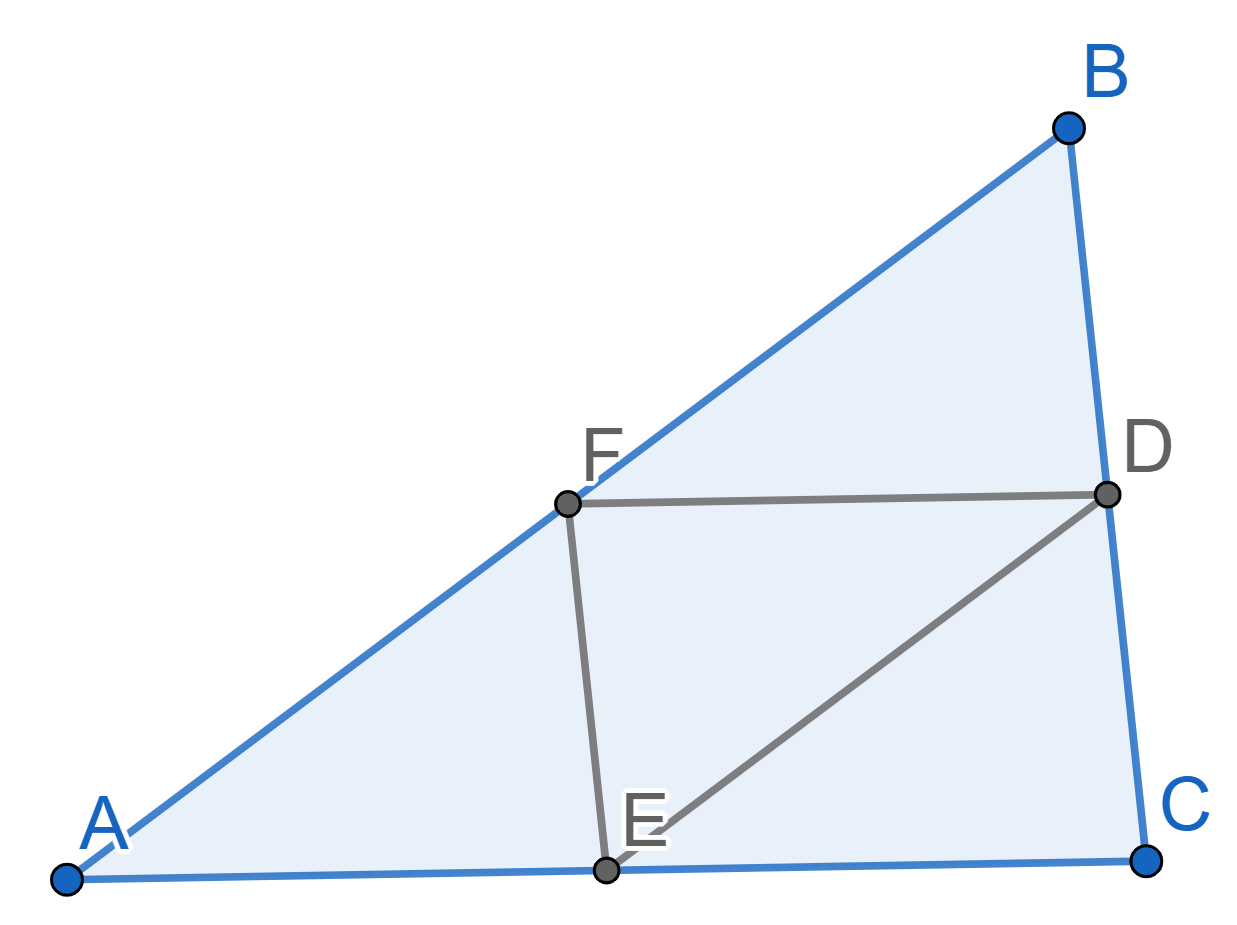
Let \(ABC\) be a triangle. Prove that the heights \(AD\), \(BE\), \(CF\) intersect in one point.

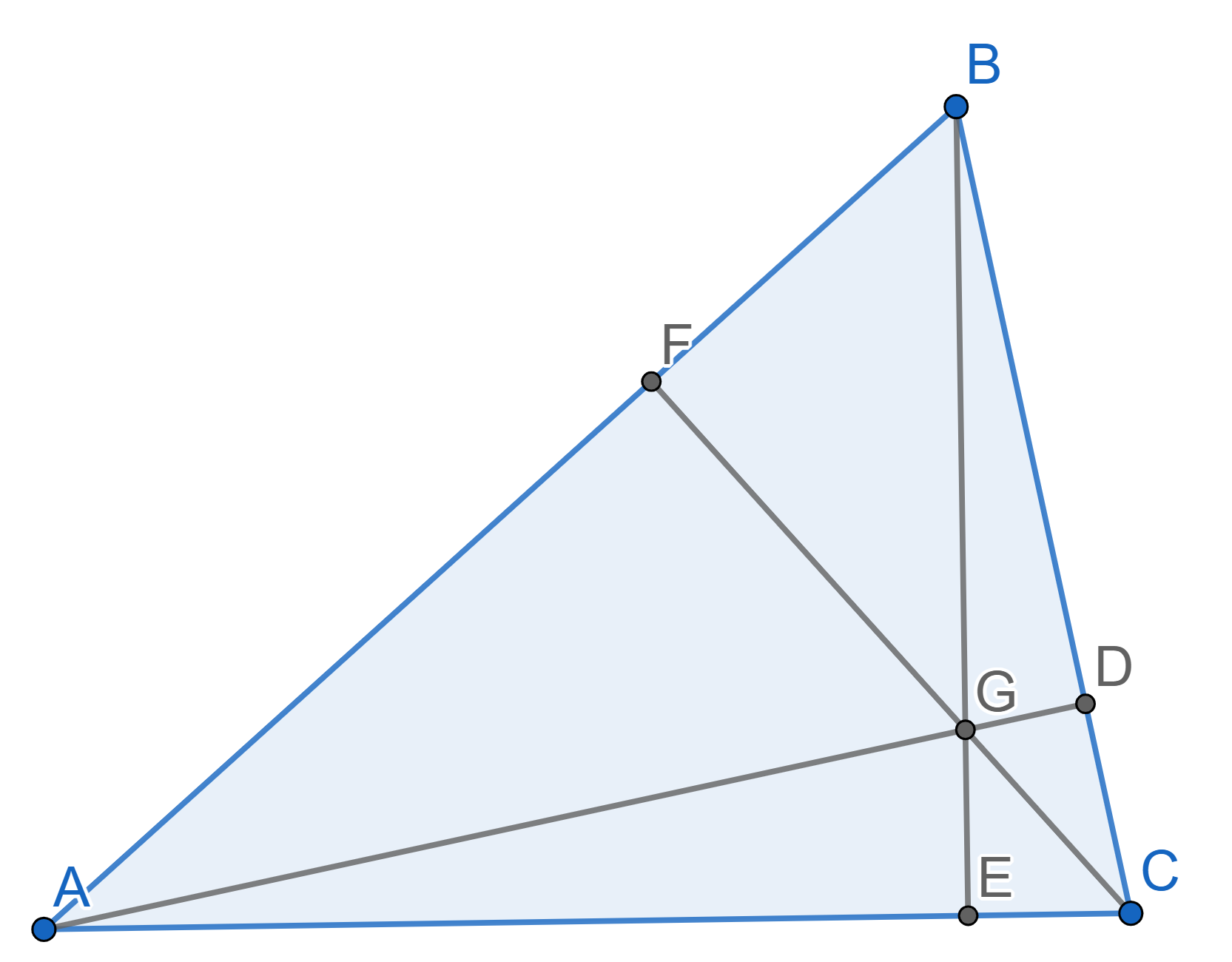
Let \(ABC\) be a triangle. Prove that the medians \(AD\), \(BE\), \(CF\) intersect in one point.

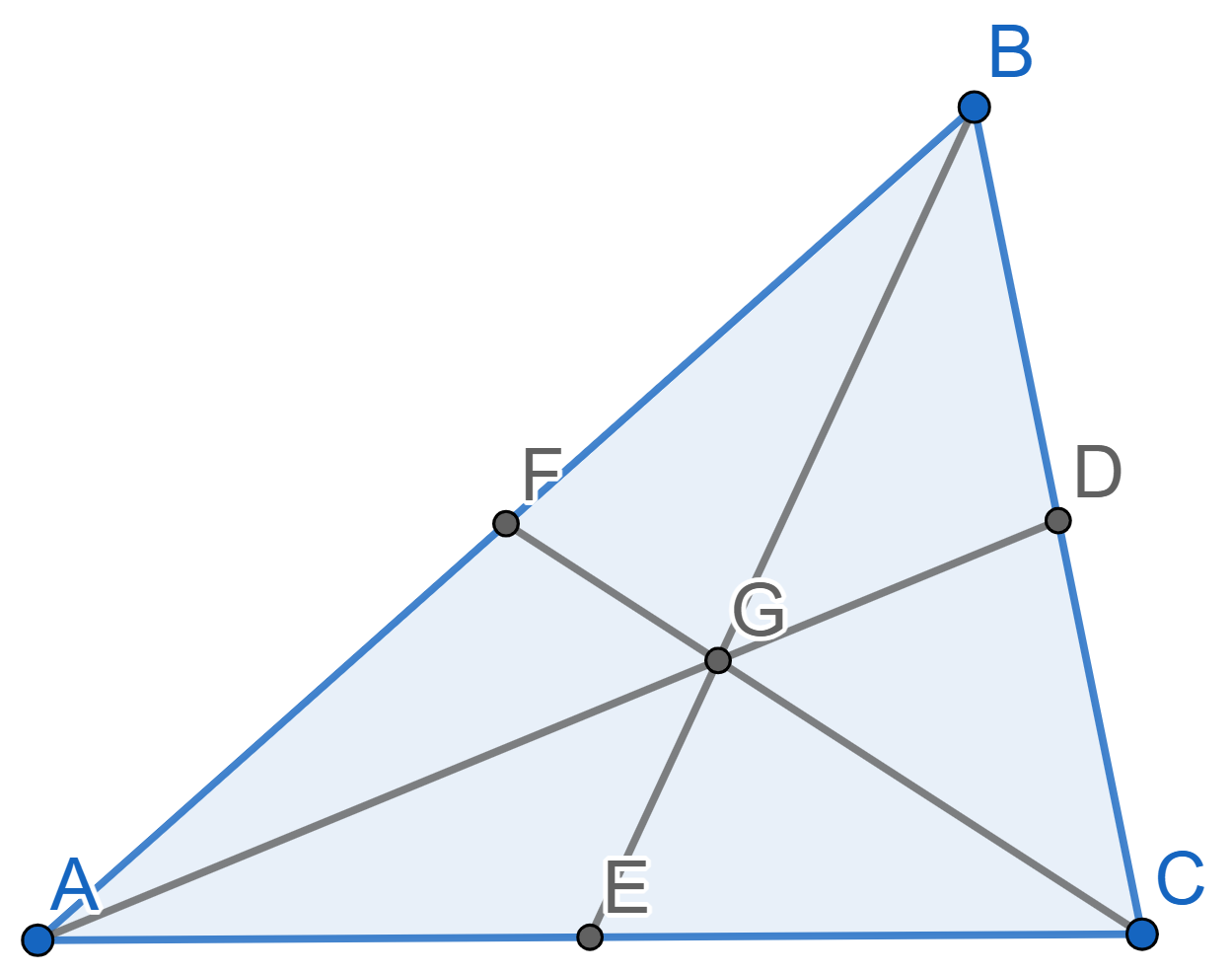
Let \(ABC\) be a triangle with medians \(AD\), \(BE\), \(CF\). Prove that the triangles \(ABC\) and \(DEF\) are similar. What is their similarity coefficient?

How many subsets are there of \(\{1,2,...,10\}\) (the integers from \(1\) to \(10\) inclusive) containing no consecutive digits? That is, we do count \(\{1,3,6,8\}\) but do not count \(\{1,3,6,7\}\).
For example, when \(n=3\), we have \(8\) subsets overall but only \(5\) contain no consecutive integers. The \(8\) subsets are \(\varnothing\) (the empty set), \(\{1\}\), \(\{2\}\), \(\{3\}\), \(\{1,3\}\), \(\{1,2\}\), \(\{2,3\}\) and \(\{1,2,3\}\), but we exclude the final three of these.

Dario is making a pizza. He has the option to choose from \(3\) different types of flatbread, \(4\) different types of cheese and \(2\) different sauces. How many different pizzas can he make?