Problems

Consider an equilateral triangle \(ABC\). Parallel to each side, five equally spaced segments are drawn across the triangle so that \(ABC\) is subdivided into \(36\) smaller equilateral triangles. Vertices \(A,B\) and \(C\) are painted red, blue and green, respectively in counterclockwise order. Alice and Bob take turns painting each vertex of the smaller triangles either red, green, or blue with the following restrictions: the segment \(AB\) can only have red or green, the segment \(BC\) can only have green and blue, and the segment \(AC\) can only have blue and red. The interior vertices can be drawn freely. Once all vertices have been painted, Alice gets a point for every smaller triangle whose vertices have the three colors (red, green, and blue) appearing in the counterclockwise direction. Bob gets a point for every smaller triangle whose vertices have the three colors but in the clockwise direction. Who wins?

There are \(100\) people in a room, and each person has at least one friend in the room. Prove that amongst them there are two people with the same number of friends in the room (we don’t count being friends with oneself).

Suppose that \((x_1,y_1),(x_2,y_2)\) are solutions to Pell’s equation \(x^2-dy^2 = 1\). Show that \((x_1x_2+dy_1y_2,x_1y_2+x_2y_2)\) also satisfies the same equation.

Suppose that \(x+y\sqrt{d}>1\) gives a solution to Pell’s equation. Show that \(x\geq 2\) and \(y\geq 1\). Can the bounds be achieved?

Can we obtain the polynomial \(h(x)=x\) by adding, subtracting, or multiplying the polynomials \(f(x)=x^2+x\) and \(g(x)=x^2+2\)?

Every year the citizens of the planet “Lotsofteeth" enter a contest to see who has the most teeth.
This year the judge notices:

1. Nobody has 0 teeth (everyone has at least 1).

2. There are more people in the contest than the most teeth that any one person has. (For example, if the most teeth anyone has is 27, then there are more than 27 people participating in the contest.)

Must there be two people who have exactly the same number of teeth? Explain why.

A cube net is a 2D shape that can be folded into a cube. For example, in the following diagram we show a cube net and the steps that fold it into a cube:

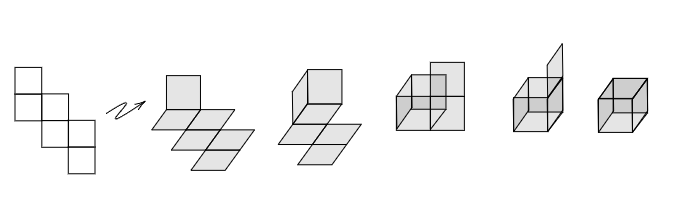
Imagine that you want to cover an endless floor with this cube net, so there are no gaps or overlaps, how would you lay them out? This is called covering or tiling the plane.

Cut a square into three parts and then use these three pieces to form a triangle such that:

1. All its angles are acute (i.e: less than \(90^\circ\)).

2. All its sides are of different lengths.

Jamie has a bag full of cards, where each card has a whole number written on it. How many cards must Jamie take from the bag to be certain that, among the cards chosen, there are at least two numbers whose average is also a whole number? Recall that to calculate the average of two numbers, we add them together and then divide by two.

Long before meeting Snow White, the seven dwarves lived in seven different mines. There is an underground tunnel connecting any two mines. All tunnels were separate, so you could not start in one tunnel and somehow end up in another. Is it possible to walk through every tunnel exactly once without retracing your path?