Problems
Jessica, Nicole and Alex received 6 coins between them: 3 gold coins and 3 silver coins. Each of them received 2 coins. Jessica doesn’t know which coins the others received but only which coins she has. Think of a question which Jessica can answer with either “yes”, “no” or “I don’t know” such that from the answer you can know which coins Jessica has.
Find the smallest four-digit number \(CEEM\) for which there exists a solution to the rebus \(MN + PORG = CEEM\). (The same letters correspond to the same numbers, different – different.)
A space traveller decided to visit the planet and upon arrival he met three inhabitants. The traveller asked each of the inhabitants: “How many truth tellers are there among your companions?”. The first one answered: “None.” The second one said: “One”. What did the third alien say?
A rectangle is cut into several smaller rectangles, the perimeter of each of which is an integer number of meters. Is it true that the perimeter of the original rectangle is also an integer number of meters?
At the disposal of a tile layer there are 10 identical tiles, each of which consists of 4 squares and has the shape of the letter L (all tiles are oriented the same way). Can he make a rectangle with a size of \(5 \times 8\)? (The tiles can be rotated, but you cannot turn them over). For example, the figure shows the wrong solution: the shaded tile is incorrectly oriented.
Arrange brackets and arithmetic signs around these numbers so that the correct equality is obtained: \[\frac{1}{2}\quad \frac{1}{6}\quad \frac{1}{6009} \ = \ 2003.\]
A square napkin was folded in half, the resulting rectangle was then folded in half again (see the figure). The resulting square was then cut with scissors (in a straight line). Could the napkin have been broken up a) into 2 parts? b) into 3 parts? c) into 4 parts? d) into 5 parts? If yes – illustrate such a cut, if not – write the word “no”.
A rabbit, preparing for the arrival of guests, hung lightbulbs in three corners of his polygonal hole. Winnie the Pooh and Piglet came and noticed that lights did not illuminate all the pots of honey which were in the rabbit hole. When they reached for some honey, two of the lightbulbs broke. The rabbit moved the remaining light bulb into some corner so that the whole hole was lit up. Is this possible? (If yes, draw an example, if not, justify the answer.)
The number \(A\) is positive, \(B\) is negative, and \(C\) is zero. What is the sign of the number \(AB + AC + BC\)?
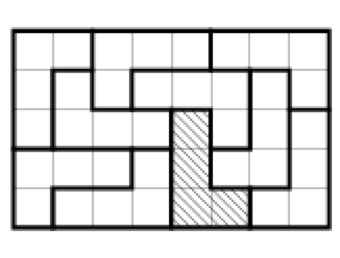
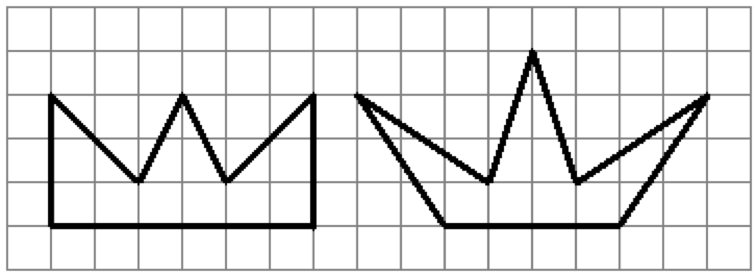
Find the area of the figures shown below.
