We solve problems

Problem #PRU-109599

Problems Calculus Number sequences Boundedness, monotonicity Algebra Number theory. Divisibility Divisibility of a number. General properties Methods Examples and counterexamples. Constructive proofs Polynomials Algebraic identities for polynomials Identical transformations Sequences Sequences

14–16 5.0

Prove that for any natural number \(a_1> 1\) there exists an increasing sequence of natural numbers \(a_1, a_2, a_3, \dots\), for which \(a_1^2+ a_2^2 +\dots+ a_k^2\) is divisible by \(a_1+ a_2+\dots+ a_k\) for all \(k \geq 1\).

Problem #PRU-109603

Problems Algebra Number theory. Divisibility Divisibility of a number. General properties Methods Examples and counterexamples. Constructive proofs Calculus Number sequences Number sequences (other)

14–16 5.0

Is there a sequence of natural numbers in which every natural number occurs exactly once, and for any \(k = 1, 2, 3, \dots\) the sum of the first \(k\) terms of the sequence is divisible by \(k\)?

Problem #PRU-109685

Problems Algebra Algebraic inequalities and systems of inequalities Linear inequalites and systems of inequalities Methods Proof by contradiction Calculus Real numbers Rational and irrational numbers

14–16 4.0

At all rational points of the real line, integers are arranged. Prove that there is a segment such that the sum of the numbers at its ends does not exceed twice the number on its middle.

Problem #PRU-109704

Problems Algebra Algebraic inequalities and systems of inequalities Algebraic inequalities (other) Methods Algebraic methods Counting in two ways Calculus Real numbers Integer and fractional parts. Archimedean property

13–15 4.0

Prove that for any positive integer \(n\) the inequality

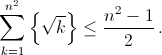
is true.

Problem #PRU-109707

Problems Calculus Functions of one variable. Continuity Certain properties of a function and recurrence relations.

14–16 4.0

Find all the functions \(f\colon \mathbb {R} \rightarrow \mathbb {R}\) which satisfy the inequality \(f (x + y) + f (y + z) + f (z + x) \geq 3f (x + 2y + 3z)\) for all \(x, y, z\).

Problem #PRU-109715

Problems Algebra Sequences Progressions Geometric progression Calculus Real numbers Integer and fractional parts. Archimedean property Sums of number sequences and difference series

13–15 4.0

Find the sum \(1/3 + 2/3 + 2^2/3 + 2^3/3 + \dots + 2^{1000}/3\).

Problem #PRU-109748

Problems Geometry Plane geometry Convex and non-convex figures Convex polygons Combinatorics Painting problems Methods Pigeonhole principle Pigeonhole principle (finite number of poits, lines etc.) Polygons Polygons (other)

13–15 4.0

We are given a convex 200-sided polygon in which no three diagonals intersect at the same point. Each of the diagonals is coloured in one of 999 colours. Prove that there is some triangle inside the polygon whose sides lie some of the diagonals, so that all 3 sides are the same colour. The vertices of the triangle do not necessarily have to be the vertices of the polygon.

Problem #PRU-109754

Problems Geometry Solid geometry Visual geometry in space

11–13 2.0

Prove that for all \(x \in (0;\pi /2)\) for \(n > m\), where \(n, m\) are natural, we have the inequality \(2 | \sin^n x-\cos^n x | \leq 3 | \sin^m x-\cos^m x |\);

Problem #PRU-109766

Problems Algebra Word Problems Tables and tournaments Number tables and its properties Methods Pigeonhole principle Pigeonhole principle (other)

12–14 4.0

Is it possible to arrange natural numbers from 1 to \(2002^2\) in the cells of a \(2002\times2002\) table so that for each cell of this table one could choose a triplet of numbers, from a row or column, where one of the numbers is equal to the product of the other two?

Problem #PRU-109780

Problems Calculus Real numbers Set theory and logic Set theory

14–16 4.0

A number set \(M\) contains \(2003\) distinct positive numbers, such that for any three distinct elements \(a, b, c\) in \(M\), the number \(a^2 + bc\) is rational. Prove that we can choose a natural number \(n\) such that for any \(a\) in \(M\) the number \(a\sqrt{n}\) is rational.