Problems

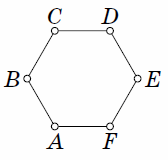
At the vertices of the hexagon \(ABCDEF\) (see Fig.) There were 6 identical balls: at \(A\) – one with mass 1 g, at \(B\) – 2 g, ..., at \(F\) – 6 g. Callum changed the places of two balls in opposite vertices. A set of weighing scales with 2 plates is available, which let you know which plate contains the balls of greater mass. How, in one weighing, can it be determined which balls were rearranged?

There are 40 weights of weights of 1 g, 2 g, ..., 40 grams. Of these, 10 weights of even weight were chosen and placed on the left hand side of the scales. Then we selected 10 weights of odd weight and put it on the right hand side of the scales. The scales were balanced. Prove that on one of the bowls of the scales there are two weights with a mass difference of 20 g.

Mark has 1000 identical cubes, each of which has one pair of opposite faces which are coloured white, another pair which are blue and a third pair that are red. He made a large \(10 \times 10 \times 10\) cube from them, joining cubes to one another which have the same coloured faces. Prove that the large cube has a face which is solidly one colour.

Two ants crawled along their own closed route on a \(7\times7\) board. Each ant crawled only on the sides of the cells of the board and visited each of the 64 vertices of the cells exactly once. What is the smallest possible number of cell edges, along which both the first and second ants crawled?

101 random points are chosen inside a unit square, including on the edges of the square, so that no three points lie on the same straight line. Prove that there exist some triangles with vertices on these points, whose area does not exceed 0.01.

In six baskets there are pears, plums and apples. The number of plums in each basket is equal to the total number of apples in the other baskets. The number of apples in each basket is equal to the total number of pears in the other baskets. Prove that the total number of fruits is divisible by 31.

Solve the following inequality: \(x+y^2 +\sqrt{x-y^2-1} \leq 1\).

The function \(f (x)\) is defined on the positive real \(x\) and takes only positive values. It is known that \(f (1) + f (2) = 10\) and \(f(a+b) = f(a) + f(b) + 2\sqrt{f(a)f(b)}\) for any \(a\) and \(b\). Find \(f (2^{2011})\).

On a chessboard, \(n\) white and \(n\) black rooks are arranged so that the rooks of different colours cannot capture one another. Find the greatest possible value of \(n\).

Is it true that, if \(b>a+c>0\), then the quadratic equation \(ax^2 +bx+c=0\) has two roots?