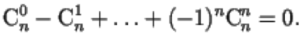Problems
A pawn stands on one of the squares of an endless in both directions chequered strip of paper. It can be shifted by \(m\) squares to the right or by \(n\) squares to the left. For which \(m\) and \(n\) can it move to the next cell to the right?
Solve the equations \(x^2 = 14 + y^2\) in integers.
Solve the equation with integers \(x^2 + y^2 = 4z - 1\).
Let \(p\) be a prime number, and \(a\) an integer number not divisible by \(p\). Prove that there is a positive integer \(b\) such that \(ab \equiv 1 \pmod p\).
a) Two students need to be chosen to participate in a mathematical Olympiad from a class of 30 students. In how many ways can this be done?
b) In how many ways can a team of three students in the same class be chosen?
How many ways can Susan choose 4 colours from 7 different ones?
On the plane, 10 points are marked so that no three of them lie on the same line. How many triangles are there with vertices at these points?
A person has 10 friends and within a few days invites some of them to visit so that his guests never repeat (on some of the days he may not invite anyone). How many days can he do this for?
Prove that out of \(n\) objects an even number of objects can be chosen in \(2^{n-1}\) ways.
