We solve problems

Problem #PRU-109573

Problems Calculus Real numbers Integer and fractional parts. Archimedean property Methods Pigeonhole principle Pigeonhole principle (angles and lengths)

13–15 3.0

Prove that for all \(x\), \(0 < x < \pi /3\), we have the inequality \(\sin 2x + \cos x > 1\).

Problem #PRU-109574

Problems Methods Mathematical induction Mathematical induction (other) Pigeonhole principle Pigeonhole principle (other)

13–16 4.0

On a particular day it turned out that every person living in a particular city made no more than one phone call. Prove that it is possible to divide the population of this city into no more than three groups, so that within each group no person spoke to any other by telephone.

Problem #PRU-109603

Problems Number Theory Divisibility Divisibility of a number. General properties Methods Examples and counterexamples. Constructive proofs Calculus Number sequences Number sequences (other)

14–16 5.0

Is there a sequence of natural numbers in which every natural number occurs exactly once, and for any \(k = 1, 2, 3, \dots\) the sum of the first \(k\) terms of the sequence is divisible by \(k\)?

Problem #PRU-109685

Problems Algebra Algebraic inequalities and systems of inequalities Linear inequalites and systems of inequalities Methods Proof by contradiction Calculus Real numbers Rational and irrational numbers

14–16 4.0

At all rational points of the real line, integers are arranged. Prove that there is a segment such that the sum of the numbers at its ends does not exceed twice the number on its middle.

Problem #PRU-109704

Problems Algebra Algebraic inequalities and systems of inequalities Algebraic inequalities (other) Methods Algebraic methods Counting in two ways Calculus Real numbers Integer and fractional parts. Archimedean property

13–15 4.0

Prove that for any positive integer \(n\) the inequality

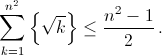
is true.

Problem #PRU-109748

Problems Geometry Plane geometry Convex and non-convex figures Convex polygons Discrete Mathematics Combinatorics Painting problems Methods Pigeonhole principle Pigeonhole principle (finite number of poits, lines etc.) Polygons Polygons (other)

13–15 4.0

We are given a convex 200-sided polygon in which no three diagonals intersect at the same point. Each of the diagonals is coloured in one of 999 colours. Prove that there is some triangle inside the polygon whose sides lie some of the diagonals, so that all 3 sides are the same colour. The vertices of the triangle do not necessarily have to be the vertices of the polygon.

Problem #PRU-109766

Problems Fun Problems Word Problems Tables and tournaments Number tables and its properties Methods Pigeonhole principle Pigeonhole principle (other)

12–14 4.0

Is it possible to arrange natural numbers from 1 to \(2002^2\) in the cells of a \(2002\times2002\) table so that for each cell of this table one could choose a triplet of numbers, from a row or column, where one of the numbers is equal to the product of the other two?

Problem #PRU-109808

Problems Discrete Mathematics Combinatorics Geometry on grid paper Integer lattices Integer lattices (other) Painting problems Methods Pigeonhole principle Pigeonhole principle (finite number of poits, lines etc.)

12–14 3.0

All of the points with whole number co-ordinates in a plane are plotted in one of three colours; all three colours are present. Prove that there will always be possible to form a right-angle triangle from these points so that its vertices are of three different colours.

Problem #PRU-109834

Problems Methods Colouring Colouring (other) Calculus Real numbers Rational and irrational numbers

14–16 5.0

Ten pairwise distinct non-zero numbers are such that for each two of them either the sum of these numbers or their product is a rational number.

Prove that the squares of all numbers are rational.

Problem #PRU-109877

Problems Methods Pigeonhole principle Pigeonhole principle (finite number of poits, lines etc.)

11–13 3.0

A regular hexagon with sides of length \(5\) is divided by straight lines, that are parallel to its sides, to form regular triangles with sides of length 1. We call the vertices of all such triangles nodes. It is known that more than half of the nodes are marked. Prove that there are five marked nodes lying on one circle.