Problems

Among 4 people there are no three with the same name, the same middle name and the same surname, but any two people have either the same first name, middle name or surname. Can this be so?

Theorem: All people have the same eye color.

"Proof" by induction: This is clearly true for one person.

Now, assume we have a finite set of people, denote them as \(a_1,\, a_2,\, ...,\,a_n\), and the inductive hypothesis is true for all smaller sets. Then if we leave aside the person \(a_1\), everyone else \(a_2,\, a_3,\,...,\,a_n\) has the same color of eyes and if we leave aside \(a_n\), then all \(a_1,\, a_2,\,a_3,...,\,a_{n-1}\) also have the same color of eyes. Thus any \(n\) people have the same color of eyes.
Find a mistake in this "proof".

Nick has written in some order all the numbers \(1,2,...33\) at the vertices of a regular \(33\)-gon. His little sister Hannah assigned to each side of the \(33\)-gon the number equal to the sum of the numbers at the ends of that side. It turns out that Hannah obtained \(33\) consecutive numbers in certain order. Can you find an arrangement of numbers as written by Nick which lead to this situation?

Is it possible to arrange the numbers \(1,\, 2,\, ...,\, 50\) at the vertices and middles of the sides of a regular \(25\)-gon so that the sum of the three numbers at the ends and in the middle of each side is the same for all sides?

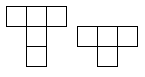
Draw a shape that can be cut into \(4\) copies of the figure on the left or into \(5\) copies of the figure on the right (the figures can be rotated).

There are 8 students in an online chess club. Show that some two of them were born on the same day of the week.

Ramesh has an infinite number of red, blue and green socks in his drawer. How many socks does he need to pick from the drawer at random to guarantee he will have at least one pair of socks of one colour?

There are \(6\) people playing a game online together. Among any \(3\) people at least \(2\) people know each other. Show that there is a group of \(3\) people that all know each other.

On a certain planet the time zones can only differ by a multiple of \(1\) hour and their day is divided into hours in the same way Earth’s day is divided into hours. Show that if we pick \(25\) cities on that planet, some two cities will have the same local time.

A bag contains balls of two different colours: black and white. What is the smallest number of balls that needs to be taken out of the bag blindly so that among them there are obviously two balls of the same colour?