Problems
Alice took a red marker and marked 5 points with integer coordinates on a coordinate plane. Miriam took a blue marker and marked a midpoint for each pair of red points. Prove that at least 1 of the blue points has integer coordinates.
Each point on a circle was painted either red or green. Show that there is an isosceles triangle whose vertices are on the circumference of the circle, such that all three vertices are red or all three are green.
Will and Neal are writing numbers on the blackboard. Each number is only composed of digits \(0\) and \(1\) in its decimal representation (as in, normal base 10 numbers). Will then says “I wonder if there is such a number we could write that can be divided by \(2018\)". Is there?
Anna has a garden shaped like an equilateral triangle of side \(8\) metres. She wants to plant \(17\) plants, but they need space – they need to be at least \(2\) metres apart in order for their roots to have access to all the microelements in the ground. Show that Anna’s garden is unfortunately too small.
A math circle student Emilio wrote a computer program for his house robot, Basil. Starting from 1, Basil should keep writing bigger and bigger numbers formed by 1s: 1, 11, 111, etc. The program terminates when Basil writes a number that is a multiple of 19. Prove that the program will terminate in fewer than 20 steps.
Orcs and goblins, 40 creatures altogether, are standing in a rectangular formation of \(4\) rows and \(10\) columns. Is it possible that the total number of orcs in each row is \(7\), while the number of orcs in each column is the same?
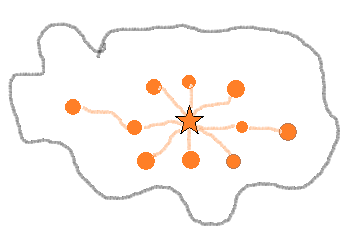
There are some cannons in every fortress on Cannon Island. The star marks the Grand Fortress, the capital, and the \(10\) circles mark \(10\) smaller fortresses. The total number of cannons located in all the fortresses along the east-west road is known to be \(130\). The total number of cannons along each of the other three roads is \(80\). Also it is known that there is a total of \(280\) cannons in all the fortresses. How many cannons are in the capital?
There are \(5\) directors of \(5\) banks sitting at the round table. Some of these banks have a negative balance (they owe more money than they have) and some have a positive balance (they have more money than they owe). It is known that for any 3 directors sitting next to each otehr, their 3 banks together have a positive balance. Does this mean that the \(5\) banks together have a positive balance?
A group of Martians and a group of Venusians got together for an important talk. At the start of the meeting, each Martian shook hands with 6 different Venusians, and each Venusian shook hands with 8 different Martians. It is known that 24 Martians took part in the meeting. How large was the delegation for Venus?
There are \(36\) warrior tomcats standing in a \(6 \times 6\) square formation. Each cat has several daggers strapped to his belt. Is it possible that the total number of daggers in each row is more than \(50\) and the total number of daggers in each column is less than \(50\)?