We solve problems

Problem #PRU-103791

Problems Number Theory Numeral systems Decimal number system Discrete Mathematics Set theory and logic Mathematical logic Puzzles

12–12 3.0

In the rebus below, replace the letters with numbers such that the same numbers are represented with the same letter. The asterisks can be replaced with any numbers such that the equations hold.

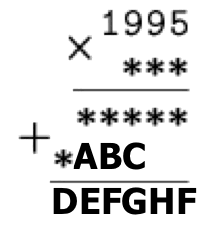
An explanation of the notation used: the unknown numbers in the third and fourth rows are the results of multiplying 1995 by each digit of the number in the second row, respectively. These third and fourth rows are added together to get the total result of the multiplication \(1995 \times ***\), which is the number in the fifth row. This is an example of a “long multiplication table”.

Problem #PRU-103802

Problems Number Theory Numeral systems Decimal number system Divisibility Divisibility of a number. General properties Discrete Mathematics Set theory and logic Set theory Set cardinality. One-to-one correspondence

12–13 2.0

Which five-digit numbers are there more of: ones that are not divisible by 5 or those with neither the first nor the second digit on the left being a five?

Problem #PRU-103812

Problems Number Theory Arithmetic operations. Number identities Discrete Mathematics Set theory and logic Mathematical logic Puzzles

11–11 2.0

Alex laid out an example of an addition of numbers from cards with numbers on them and then swapped two cards. As you can see, the equality has been violated. Which cards did Alex rearrange?

Problem #PRU-103858

Problems Number Theory Divisibility The fundamental theorm of arithmetic. Prime factorisation.

12–13 2.0

Solve the rebus: \(AX \times UX = 2001\).

Problem #PRU-103946

Problems Number Theory Arithmetic operations. Number identities

11–12 2.0

The number \(A\) is positive, \(B\) is negative, and \(C\) is zero. What is the sign of the number \(AB + AC + BC\)?

Problem #PRU-103964

Problems Number Theory Divisibility Division with remainders. Arithmetic of remainders Arithmetic of remainders Methods Pigeonhole principle Pigeonhole principle (other)

12–14 3.0

There are \(n\) integers. Prove that among them either there are several numbers whose sum is divisible by \(n\) or there is one number divisible by \(n\) itself.

Problem #PRU-104021

Problems Geometry Solid geometry Parallelepipeds Special cases of parallelepipeds Cube Number Theory Divisibility Odd and even numbers Methods Pigeonhole principle Pigeonhole principle (other)

12–13 2.0

a) A 1 or a 0 is placed on each vertex of a cube. The sum of the 4 adjacent vertices is written on each face of the cube. Is it possible for each of the numbers written on the faces to be different?

b) The same question, but if 1 and \(-1\) are used instead.

Problem #PRU-104075

Problems Number Theory Numeral systems Decimal number system Methods Trial and error

10–12 2.0

The digits of a 3 digit number \(A\) were written in reverse order and this is the number \(B\). Is it possible to find a value of \(A\) such that the sum of \(A\) and \(B\) has only odd numbers as its digits?

Problem #PRU-104079

Problems Number Theory Numeral systems Decimal number system Methods Trial and error

10–12 2.0

Let \(x\) be a 2 digit number. Let \(A\), \(B\) be the first (tens) and second (units) digits of \(x\), respectively. Suppose \(A\) is twice as large as \(B\). If we add the square of \(A\) to \(x\) then we get the square of a certain whole number. Find the value of \(x\).

Problem #PRU-107749

Problems Number Theory Numeral systems Decimal number system Algebra Algebraic equations and systems of equations Diophantine equations

13–15 3.0

The student did not notice the multiplication sign between two three-digit numbers and wrote one six-digit number, which turned out to be seven times bigger than their product. Determine these numbers.