Problems

A student did not notice the multiplication sign between two three-digit numbers and wrote one six-digit number, which turned out to be exactly seven times their product. Determine these numbers.

The student did not notice the multiplication sign between two seven-digit numbers and wrote one fourteen-digit number, which turned out to be three times bigger than their product. Determine these numbers.

To each pair of numbers \(x\) and \(y\) some number \(x * y\) is placed in correspondence. Find \(1993 * 1935\) if it is known that for any three numbers \(x, y, z\), the following identities hold: \(x * x = 0\) and \(x * (y * z) = (x * y) + z\).

For each pair of real numbers \(a\) and \(b\), consider the sequence of numbers \(p_n = \lfloor 2 \{an + b\}\rfloor\). Any \(k\) consecutive terms of this sequence will be called a word. Is it true that any ordered set of zeros and ones of length \(k\) is a word of the sequence given by some \(a\) and \(b\) for \(k = 4\); when \(k = 5\)?

Note: \(\lfloor c\rfloor\) is the integer part, \(\{c\}\) is the fractional part of the number \(c\).

The function \(f\) is such that for any positive \(x\) and \(y\) the equality \(f (xy) = f (x) + f (y)\) holds. Find \(f (2007)\) if \(f (1/2007) = 1\).

Replace \(a, b\) and \(c\) with integers not equal to \(1\) in the equality \((ay^b)^c = - 64y^6\), so it would become an identity.

Prove that for any natural number \(a_1> 1\) there exists an increasing sequence of natural numbers \(a_1, a_2, a_3, \dots\), for which \(a_1^2+ a_2^2 +\dots+ a_k^2\) is divisible by \(a_1+ a_2+\dots+ a_k\) for all \(k \geq 1\).

At all rational points of the real line, integers are arranged. Prove that there is a segment such that the sum of the numbers at its ends does not exceed twice the number on its middle.

Prove that for any positive integer \(n\) the inequality

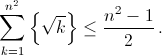
is true.

Find the sum \(1/3 + 2/3 + 2^2/3 + 2^3/3 + \dots + 2^{1000}/3\).