Alice, Bob, Claire and Daniel were playing outdoors. A mean lady told them that at least one of them has a muddy face and everyone who has a muddy face must step forward at the same time on the count of three. Then the mean lady will leave them alone.
If a child with clean face steps forward, he is punished. If nobody steps forward, then the mean lady will do the count again. The children are not allowed to signal to each other. How can Alice, Bob, Claire and Daniel avoid punishment?
A group of children were playing outdoors. A mean lady told them that at least one of them has a muddy face and everyone who has a muddy face must step forward at the same time on the count of three. Then the mean lady will leave them alone.
If a child with clean face steps forward, he is punished. If nobody steps forward, then the mean lady will do the count again. The children are not allowed to signal to each other. How can they avoid punishment?
Sperner’s lemma in dimension \(2\).
Subdivide a triangle \(ABC\)
arbitrarily into a triangulation consisting of smaller triangles meeting
edge to edge. Define Sperner coloring of the triangulation as an
assignment of three colors to the vertices of the triangulation such
that:
Each of the three vertices \(A, B,\) and \(C\) of the initial triangle has a distinct color
The vertices that lie along any edge of triangle \(ABC\) have only two colors, the two colors at the endpoints of the edge. For example, each vertex on \(AC\) must have the same color as \(A\) or \(C.\)
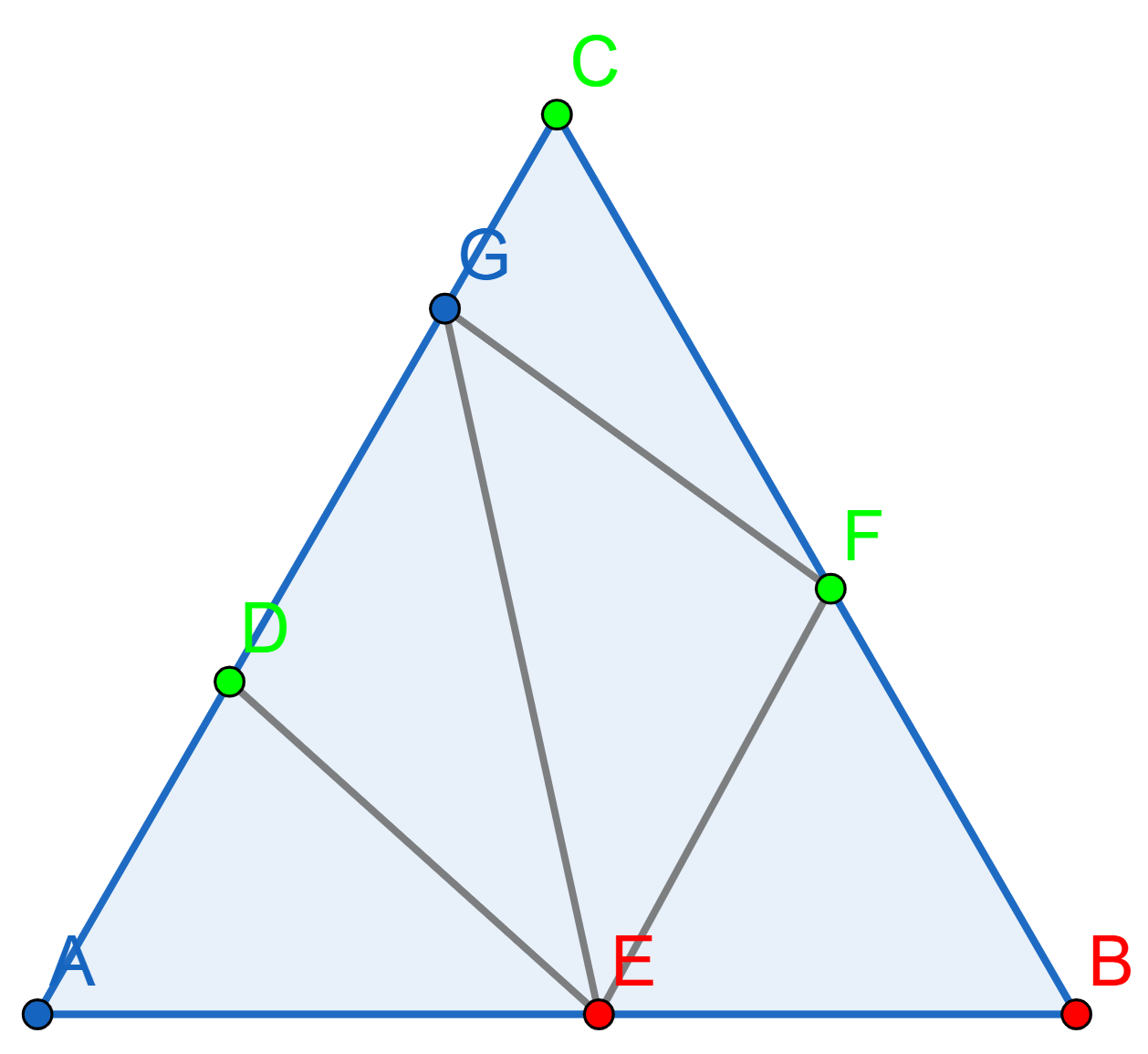
Prove that every Sperner coloring of every triangulation has at least one "rainbow triangle", a smaller triangle in the triangulation that has its vertices colored with all three different colors. More precisely, there must be an odd number of rainbow triangles.