Let \(AA_1\) and \(BB_1\) be the heights of the triangle \(ABC\). Prove that the triangles \(A_1B_1C\) and \(ABC\) are similar.
Let \(G,F,H\) and \(I\) be the midpoints of the sides \(CD, DA, AB, BC\) of the square \(ABCD\), whose area is equal to \(S\). Find the area of the quadrilateral formed by the straight lines \(BG,DH,AF,CE\).
a) Prove that if in the triangle the median coincides with the height then this triangle is an isosceles triangle.
b) Prove that if in a triangle the bisector coincides with the height then this triangle is an isosceles triangle.
Prove that the bisectors of a triangle intersect at one point.
A circle divides each side of a triangle into three equal parts. Prove that this triangle is regular.
Prove that the area \(S_{ABC}\) of a triangle is equal to \(abc/4R\).
The point \(D\) lies on the base \(AC\) of the isosceles triangle \(ABC\). Prove that the radii of the circumscribed circles of the triangles \(ABD\) and \(CBD\) are equal.
Express the area of the triangle \(ABC\) through the length of the side \(BC\) and the angles \(B\) and \(C\).
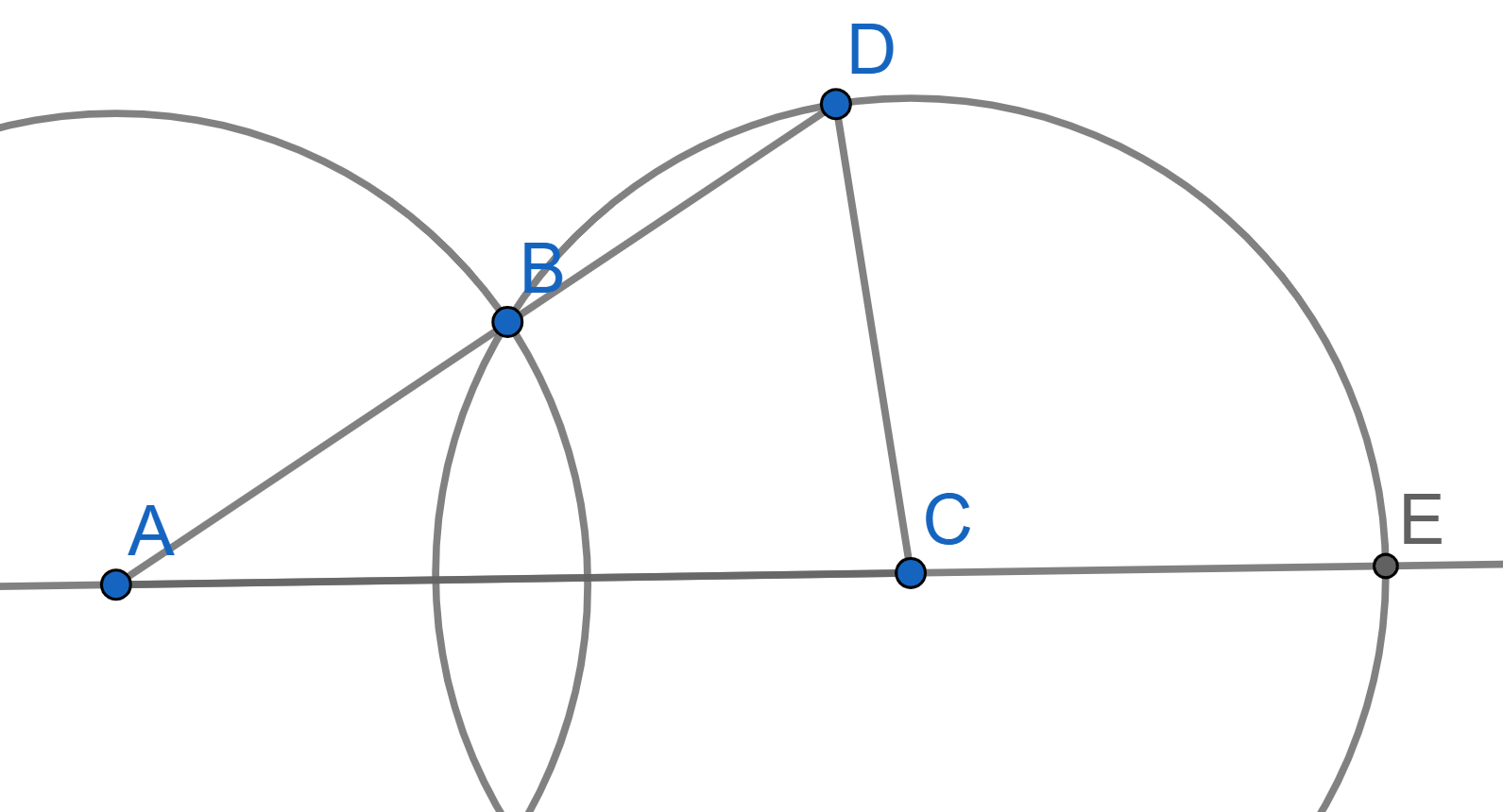
Two intersecting circles of radius \(R\) are given, and the distance between their centers is greater than \(R\). Prove that \(\beta = 3\alpha\) (Fig.).
Find all triangles in which the angles form an arithmetic progression, and the sides form: a) an arithmetic progression; b) a geometric progression.