Problems

a) There are six points on a plane. No matter which five points you choose you can cross them with two lines but one cannot find two lines which cross all six of them. Does such configuration exist?

(b) One extremely successful businesswoman is planning to build a garden in her country house. She wants to have 10 garden beds and several lanes built. She requested her architect to organize the garden in such a way that for every nine beds there are three lanes passing by them (for each garden bed out of these nine beds there is a lane among the three lanes which passes by it). On top of that she demanded that there should not be three lanes which pass by all 10 garden beds. How can the poor architect satisfy this requirement? All lanes have to be straight.

(c) A neighbour of the businesswoman is inspired by her exotic demands. He decides to surpass her on this field. The neighbour plans to build 55 garden beds. They have to be joined by several lanes in such a way that for every 54 garden beds you can find nine lanes crossing them (for each garden bed out of these 54 beds there is a lane among the nine lanes which crosses this bed). Can you help the colleague of the architect? Again all the lanes have to be straight.

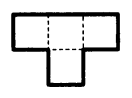
Two figures are said to be similar if all their corresponding sides are congruent and corresponding angles are equal. By using several copies of the figure below construct a bigger figure that is similar.

Divide a square into several triangles in such a way that every triangle shares a boundary with exactly three other triangles.

A maths teacher draws a number of circles on a piece of paper. When she shows this piece of paper to the young mathematician, he claims he can see only five circles. The maths teacher agrees. But when she shows the same piece of paper to another young mathematician, he says that there are exactly eight circles. The teacher confirms that this answer is also correct. How is that possible and how many circles did she originally draw on that piece of paper?

It is easy to construct one equilateral triangle from three identical matches. Can we make four equilateral triangles by adding just three more matches identical to the original ones?

In a trapezium \(ABCD\), the side \(AB\) is parallel to the side \(CD\). Show that the areas of triangles \(\triangle ABC\) and \(\triangle ABD\) are equal.

The triangle visible in the picture is equilateral. The hexagon inside is a regular hexagon. If the area of the whole big triangle is \(18\), find the area of the small blue triangle.

On the left there is a circle inscribed in a square of side 1. On the right there are 16 smaller, identical circles, which all together fit inside a square of side 1. Which area is greater, the yellow or the blue one?

In a pentagon \(ABCDE\), diagonal \(AD\) is parallel to the side \(BC\) and the diagonal \(CE\) is parallel to the side \(AB\). Show that the areas of the triangles \(\triangle ABE\) and \(\triangle BCD\) are the same.

Which triangle has the largest area? The dots form a regular grid.