Problems

Imagine you have a cube (a box with six square sides). First, cut 16 identical colourful rectangular paper strips of any size you like (choose one size and make all 16 the same). Can you cover the entire outside surface of the cube with these strips, with no gaps and no overlapping? The strips may bend and wrap around edges and corners, but after cutting the 16 strips, you are not allowed to cut them again, and everything must stay on the cube’s surface. Is it possible? Explain why or why not. (For example, two of the strips may look like this:

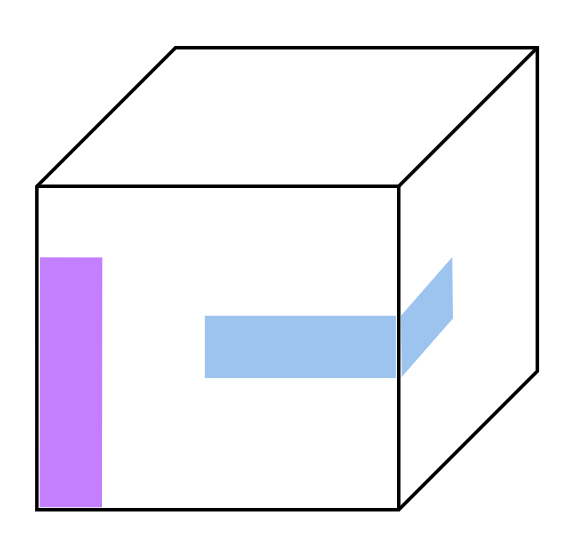
The cube from Example 3 is a present and one layer of a gift-wrap is totally not enough. Can you cover it with another 15 identical rectangles? You can assume the covering from Example 3 was thin and it did not affect the shape of a cube. As before no overlappings are allowed and the surface has to be fully covered by rectangles.

Can a \(5\times5\) square checkerboard be covered by \(1\times2\) dominoes?

Cut an equilateral triangle into 4 smaller equilateral triangles. Then can another equilateral triangle be cut into 7 smaller equilateral triangles (triangles do not necessarily have to be identical)?

Consider another equilateral triangle. Is it possible to cut it into (a) 9; (b) 16; (c) 28; (d) 2; (e) 42 smaller equilateral triangles (which are not necessarily identical)?

(f) Kyle claims he can cut an equilateral triangle into any number of smaller (not necessarily identical) equilateral triangles if this number is either greater than 8 and divisible by 3, or greater than 3 and has remainder 1 when divided by 3. Prove or disprove Kyle’s statement.

(g)* Let \(n\) be a natural number greater than 5. Is it true one can cut an equilateral triangle into \(n\) smaller equilateral triangles?

a) What is the answer in case we are asked to split the figure below into \(1\times4\) rectangles instead of \(1\times5\) rectangles?

(b) In the context of Example 1 what is the answer in case we are asked to split the figure into \(1\times7\) rectangles instead of \(1\times5\) rectangles?

Can you cover a \(10 \times 10\) board using only \(T\)-shaped tetraminoes?

Can you cover a \(10 \times 10\) square with \(1 \times 4\) rectangles?

Two opposite corners were removed from an \(8 \times 8\) chessboard. Can you cover this chessboard with \(1 \times 2\) rectangular blocks?

One small square of a \(10 \times 10\) square was removed. Can you cover the rest of it with 3-square \(L\)-shaped blocks?