We solve problems

Problem #PRU-98408

Problems Geometry Plane geometry Circles Central angle. Arc length and circumference Diameter, chords, and secants Chords and secants (other) Methods Pigeonhole principle Pigeonhole principle (finite number of poits, lines etc.) Polygons Regular polygons

12–14 4.0

In a regular shape with 25 vertices, all the diagonals are drawn.

Prove that there are no nine diagonals passing through one interior point of the shape.

Problem #PRU-98426

Problems Geometry Plane geometry Quadrilateral Parallelogram Special cases Rectangles and squares. Criteria and properties

11–13 3.0

A square is cut by 18 straight lines, 9 of which are parallel to one side of the square and the other 9 parallel to the other – perpendicular to the first 9 – dividing the square into 100 rectangles. It turns out that exactly 9 of these rectangles are squares. Prove that among these 9 squares there will be two that are identical.

Problem #PRU-98652

Problems Geometry Plane geometry Area Area ratio Area ratio of similar figures

11–12 1.0

The population of China is one billion people. It would seem that on a map of China with a scale of 1 : 1,000,000 (1 cm : 10 km), it would be possible to fit a million times fewer people than there is in the whole country. However, in fact, not only 1000, but even 100 people will not be able to be placed on this map. Can you explain this contradiction?

Problem #PRU-5014

Problems Geometry Dissections

10–13 3.0

Abigail’s little brother Carson found a big rectangular cake in the fridge and cut a small rectangular piece out of it.

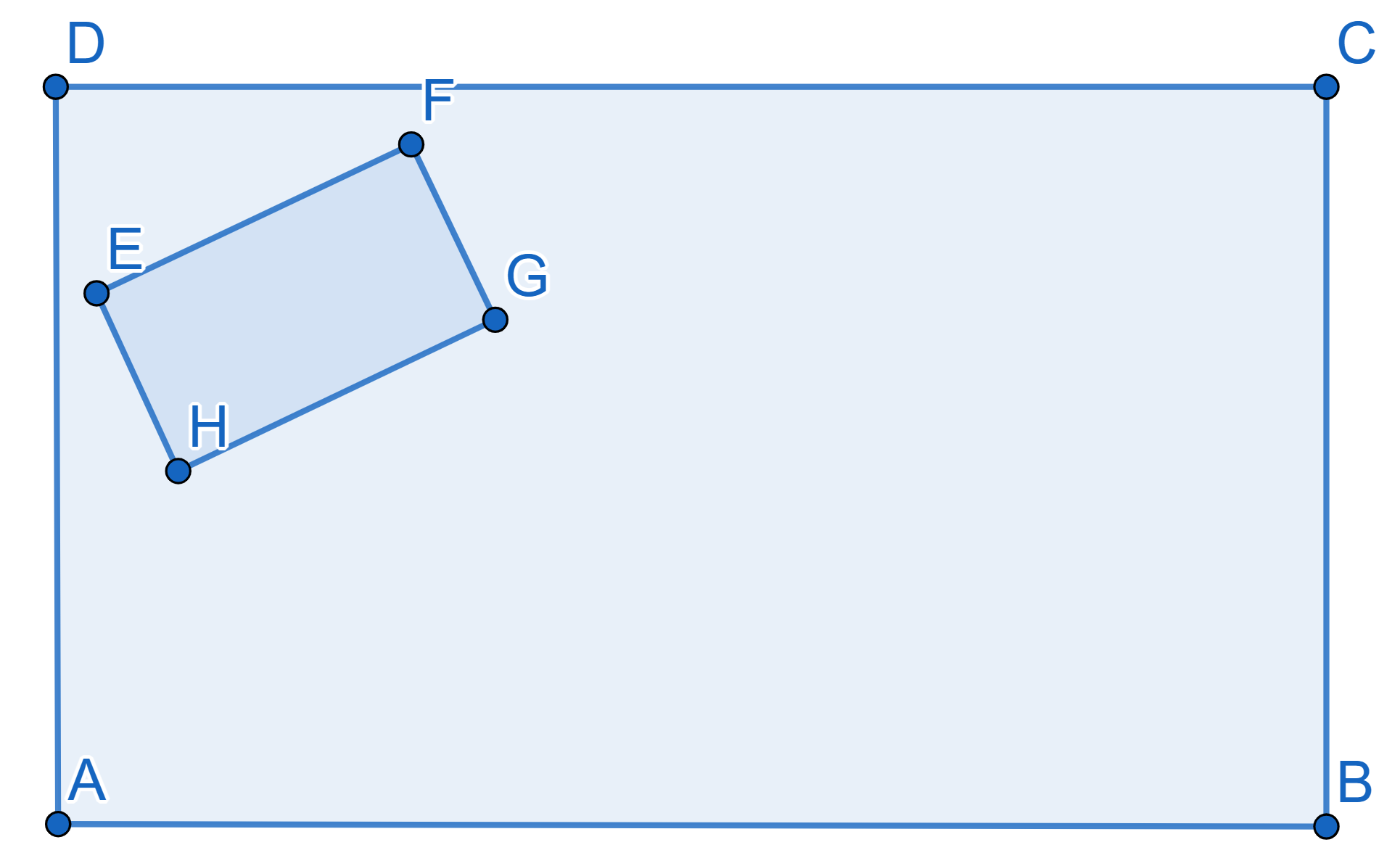
Now Abigail needs to find a way to cut the remaining cake into two pieces of equal area with only one straight cut. How could she do that? The removed piece can be of any size or orientation.

Problem #PRU-66396

Problems Geometry Combinatorial geometry

12–15 3.0

We say that a figure is convex if a segment connecting any two points lays fully within the figure. On the picture below the pentagon on the left is convex and the one on the right is not.

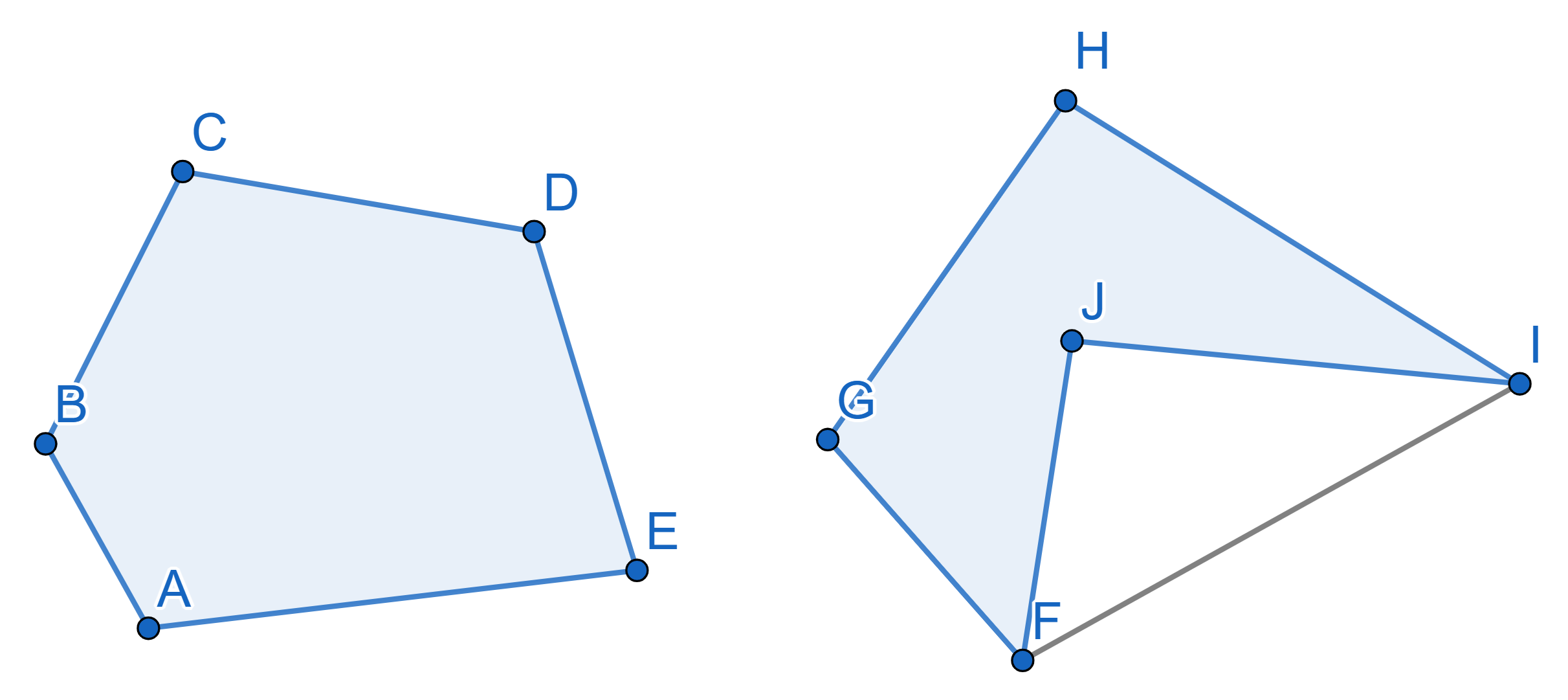
Is it possible to draw \(18\) points inside a convex pentagon so that each of the ten triangles formed by its sides and diagonals contains equal amount of points?

Problem #PRU-66548

Problems Geometry Triangles

10–15 4.0

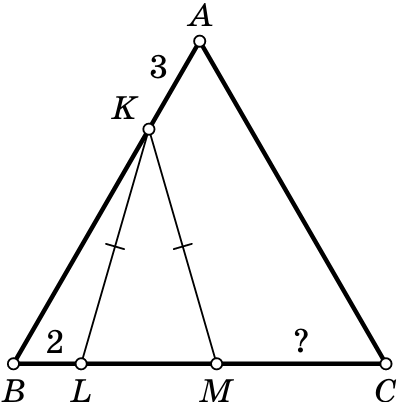
The triangle \(ABC\) is equilateral. The point \(K\) is chosen on the side \(AB\) and points \(L\) and \(M\) are on the side \(BC\) in such a way that \(L\) lies on the segment \(BM\). We have the following properties: \(KL = KM,\) \(BL = 2,\, AK = 3.\) Find the length of \(CM\).

Problem #PRU-5016

Problems Geometry Euclidean geometry

10–13 2.0

We call two figures congruent if their corresponding sides and angles are equal. Let \(ABD\) an \(A'B'D'\) be two right-angled triangles with right angle \(D\). Then if \(AD=A'D'\) and \(AB=A'B'\) then the triangles \(ABD\) and \(A'B'D'\) are congruent.
It follows from the previous statement that if two lines \(AB\) and \(CD\) are parallel than angles \(BCD\) and \(CBA\) are equal.

Problem #PRU-5017

Problems Geometry Euclidean geometry

10–13 2.0

We prove the other two assertions from the description:

The sum of all internal angles of a triangle is also \(180^{\circ}\).
In an isosceles triangle (which has two sides of equal lengths), two angles touching the third side are equal.

Problem #PRU-5018

Problems Geometry Plane geometry

10–13 2.0

In the triangle \(ABC\) the sides are compared as following: \(AC>BC>AB\). Prove that the angles are compared as follows: \(\angle B > \angle A > \angle C\).

Problem #PRU-53644

Problems Geometry Plane geometry

12–14 4.0

Consider a quadrilateral \(ABCD\). Choose a point \(E\) on side \(AB\). A line parallel to the diagonal \(AC\) is drawn through \(E\) and meets \(BC\) at \(F\). Then a line parallel to the other diagonal \(BD\) is drawn through \(F\) and meets \(CD\) at \(G\). And then a line parallel to the first diagonal \(AC\) is drawn through \(G\) and meets \(DA\) at \(H\). Prove the \(EH\) is parallel to the diagonal \(BD\).