Problems
(a) Divide 55 walnuts into four groups consisting of different number of nuts.
(b) Divide 999 walnuts into four groups consisting of different number of nuts.
Replace "stars" with different natural numbers in order to obtain an
identity:
\[\frac{1}{*}+\frac{1}{*}+\frac{1}{*}=\frac{1}{*}+\frac{1}{*}+\frac{1}{*};\]
George knows a representation of number “8” as the sum of its divisors in which only divisor “1” appears twice: \[8=4+2+1+1.\] His brother showed George that such representation exists for number “16” as well: \[16=8+4+2+1+1.\] He apologies for forgetting an example considering number “32” but he is sure once he saw such representation for this number.
(a) Help George to work out a suitable representation for number “32”;
(b) Can you think of a number which has such representation consisting of 7 terms?
(c) Of 11 terms?
(d) Can you find a number which can be represented as a sum of its divisors which are all different (pay attention that we don’t allow repeating digit “1” twice!)?
(e) What if we require this representation to consist of 11 terms?
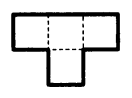
Two figures are said to be similar if all their corresponding sides
are congruent and corresponding angles are equal. By using several
copies of the figure below construct a bigger figure that is
similar.
Divide a square into several triangles in such a way that every triangle shares a boundary with exactly three other triangles.
Jennifer draws a hexagon, and a line passing through two of its vertices. It turns out one of the figures in which the original hexagon is divided is a heptagon. Show an example of a hexagon and a line for which it is true.
There are four numbers written in a row. The first number is \(100\). It is known that if we divide the first number by the second number we will get a prime number as a result, if we the second number by the third number we will get a prime number, and if we divide the third number by the fourth number we will also get a prime number. Can all the resulting prime numbers be distinct?
George claims that he knows two numbers such that their quotient is equal to their product. Can we believe him? Prove him wrong or provide a suitable example.
Can Jennifer draw an octagon and a line passing through two of its vertices in such a way that this line cuts a 10-gon from it?
In the context of Example 14.2 what is the answer if we have five numbers instead of four? (i.e., can we get four distinct prime numbers then?)