What is the ratio between the red and blue area? All shapes are semicircles.
In a parallelogram \(ABCD\), point \(E\) belongs to the side \(CD\) and point \(F\) belongs to the side \(BC\). Show that the total red area is the same as the total blue area:
The figure below is a regular pentagram. What is larger, the black area or the blue area?
A circle was inscribed in a square, and another square was inscribed in the circle. Which area is larger, the blue or the orange one?
In a square, the midpoints of its sides were marked and some segments were drawn. There is another square formed in the centre. Find its area, if the side of the square has length \(10\).
In a parallelogram \(ABCD\), point \(E\) belongs to the side \(AB\), point \(F\) belongs to the side \(CD\) and point \(G\) belongs to the side \(AD\). What is more, the marked red segments \(AE\) and \(CF\) have equal lengths. Prove that the total grey area is equal to the total black area.
Matt built a simple wooden hut to protect himself from the rain. From the side the hut looks like a right triangle with the right angle at the top. The longer part of the roof has 20 ft and the shorter one has 15 ft. What is the height of the hut in feet?
The three sides of a right triangle have all integer lengths. Show that at least one of them has an even length.
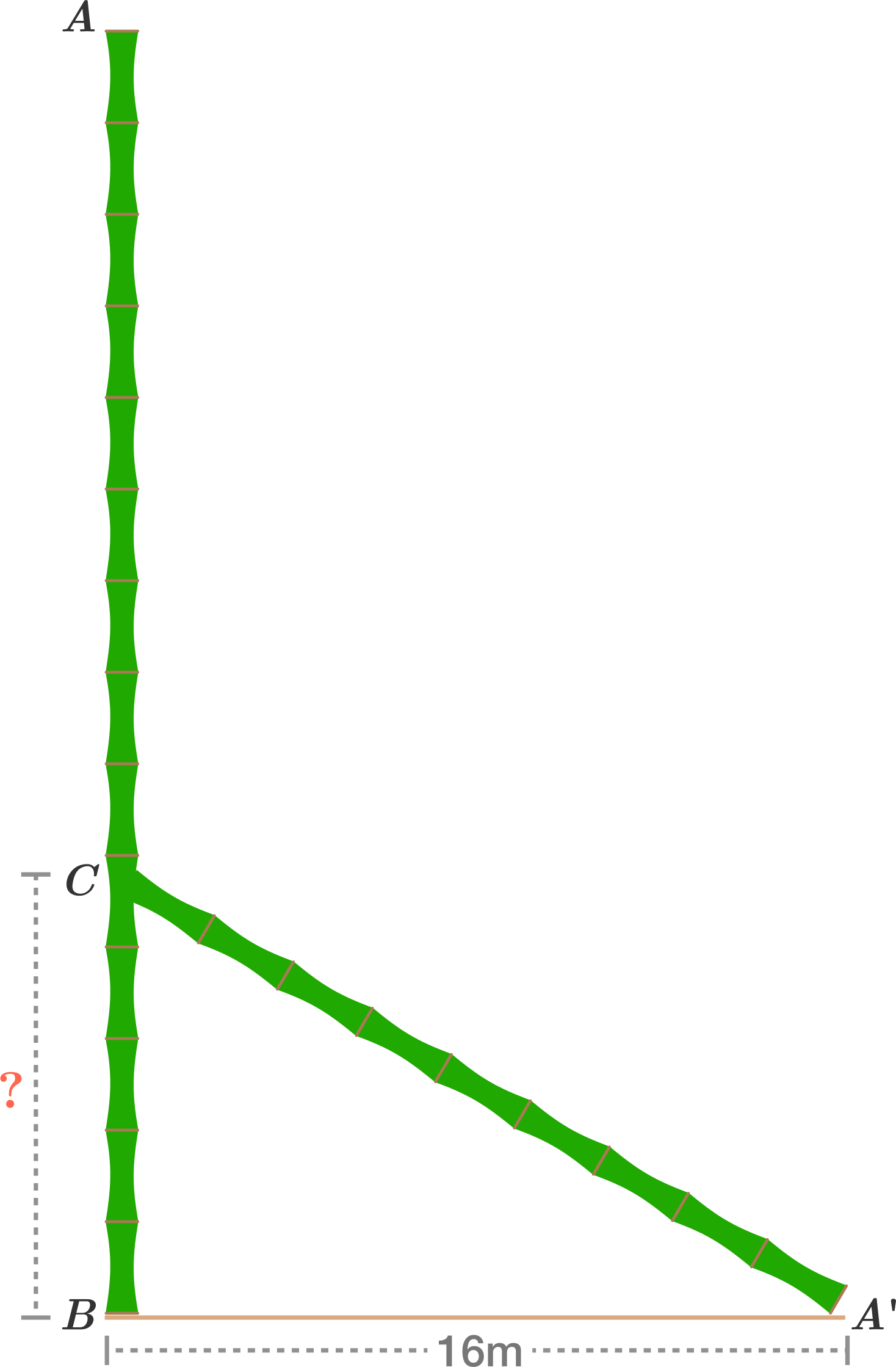
A bamboo tree, originally \(32\) metres high, broke in two parts. The end of the other one has fallen \(16\) metres far from the trunk. How high is the remaining vertical part of the bamboo tree?
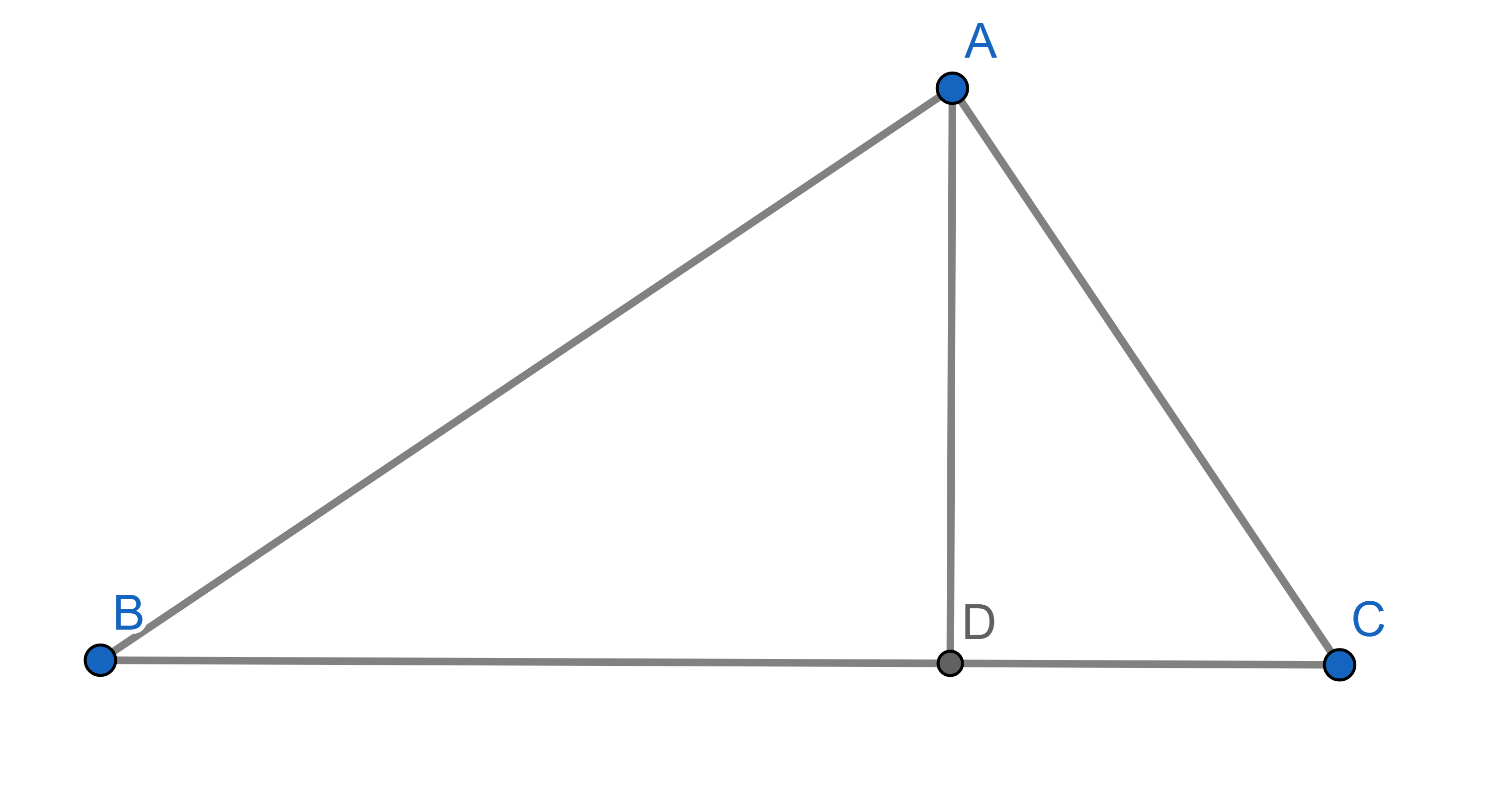
Matt has build an additional support for his hut (\(AD\)), whose length is equal to the height of the hut calculated in the Example 1. What are the distances from the base of the support to both ends of the hut? Looking at the picture, what are the distances \(BD\) and \(DC\), if \(AB = 20\) and \(AC = 15\)? Show that \(AD^2 = BD \times AC\) in this particular case. Do you think it is true in general?