Problems

When Gulliver came to Lilliput, he found that there all things were exactly 12 times shorter than in his homeland. Can you say how many Lilliputian matchboxes fit into one of Gulliver’s matchboxes?

Which rectangles with whole sides are there more of: with perimeter of 1996 or with perimeter of 1998? (The rectangles \(a \times b\) and \(b \times a\) are assumed to be the same).

A globe has 17 parallels and 24 meridians. How many parts is the globe’s surface divided into? The meridian is an arc connecting the North Pole with the South Pole. A parallel is a circle parallel to the equator (the equator is also a parallel).

A square napkin was folded in half, the resulting rectangle was then folded in half again (see the figure). The resulting square was then cut with scissors (in a straight line). Could the napkin have been broken up a) into 2 parts? b) into 3 parts? c) into 4 parts? d) into 5 parts? If yes – illustrate such a cut, if not – write the word “no”.

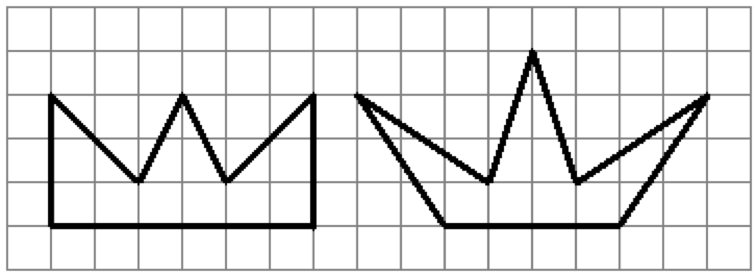
Find the area of the figures shown below.

a) A 1 or a 0 is placed on each vertex of a cube. The sum of the 4 adjacent vertices is written on each face of the cube. Is it possible for each of the numbers written on the faces to be different?

b) The same question, but if 1 and \(-1\) are used instead.

In a burrow there is a family of 24 mice. Every night exactly four of them are sent to the warehouse for cheese.

Could it occur that at some point in time each mouse went to the warehouse with every other mouse exactly one time?

In a board, 20 pins are placed (see the picture). The distance between any adjacent pins is 1 inch. Pull a string of length 19 inches from the first pin to the second one, so that it goes through all the pins.

The grasshopper jumps on the interval \([0,1]\). On one jump, he can get from the point \(x\) either to the point \(x/3^{1/2}\), or to the point \(x/3^{1/2} + (1- (1/3^{1/2}))\). On the interval \([0,1]\) the point \(a\) is chosen.

Prove that starting from any point, the grasshopper can be, after a few jumps, at a distance less than \(1/100\) from point \(a\).

All of the sweets of different sorts in stock are arranged in \(n\) boxes, for which prices are set at \(1, 2, \dots , n\), respectively. It is required to buy such \(k\) of these boxes of the least total value, which contain at least \(k/n\) of the mass of all of the sweets. It is known that the mass of sweets in each box does not exceed the mass of sweets in any more expensive box.

a) What boxes should I buy when \(n = 10\) and \(k = 3\)?

b) The same question for arbitrary natural numbers \(n \geq k\).