On weekdays, the Scattered Scientist goes to work along the circle line on the London Underground from Cannon Street station to Edgware Road station, and in the evening he goes back (see the diagram).
Entering the station, the Scientist sits down on the first train that arrives. It is known that in both directions the trains run at approximately equal intervals, and along the northern route (via Farringdon) the train goes from Cannon Street to Edgware Road or back in 17 minutes, and along the southern route (via St James Park) – 11 minutes. According to an old habit, the scientist always calculates everything. Once he calculated that, from many years of observation:
– the train going counter-clockwise, comes to Edgware Road on average 1 minute 15 seconds after the train going clockwise arrives. The same is true for Cannon Street.
– on a trip from home to work the Scientist spends an average of 1 minute less time than a trip home from work.
Find the mathematical expectation of the interval between trains going in one direction.
On one island, one tribe has a custom – during the ritual dance, the leader throws up three thin straight rods of the same length, connected in the likeness of the letter capital \(\pi\), \(\Pi\). The adjacent rods are connected by a short thread and therefore freely rotate relative to each other. The bars fall on the sand, forming a random figure. If it turns out that there is self-intersection (the first and third bars cross), then the tribe in the coming year are waiting for crop failures and all sorts of trouble. If there is no self-intersection, then the year will be successful – satisfactory and happy. Find the probability that in 2019, the rods will predict luck.
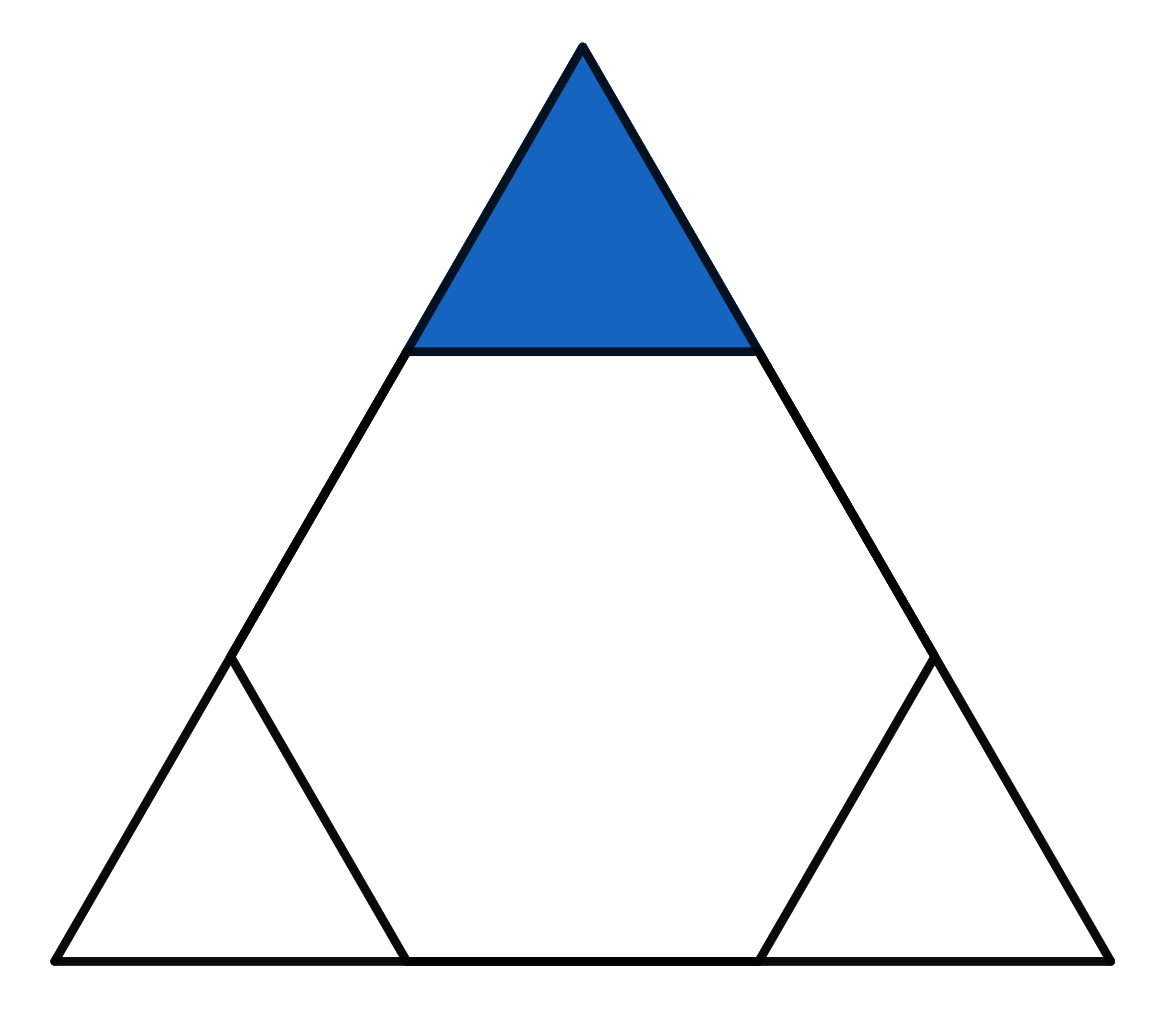
The triangle visible in the picture is equilateral. The hexagon inside is a regular hexagon. If the area of the whole big triangle is \(18\), find the area of the small blue triangle.
A quadrilateral is given; \(A\), \(B\), \(C\), \(D\) are the successive midpoints of its sides, \(P\) and \(Q\) are the midpoints of its diagonals. Prove that the triangle \(BCP\) is equal to the triangle \(ADQ\).
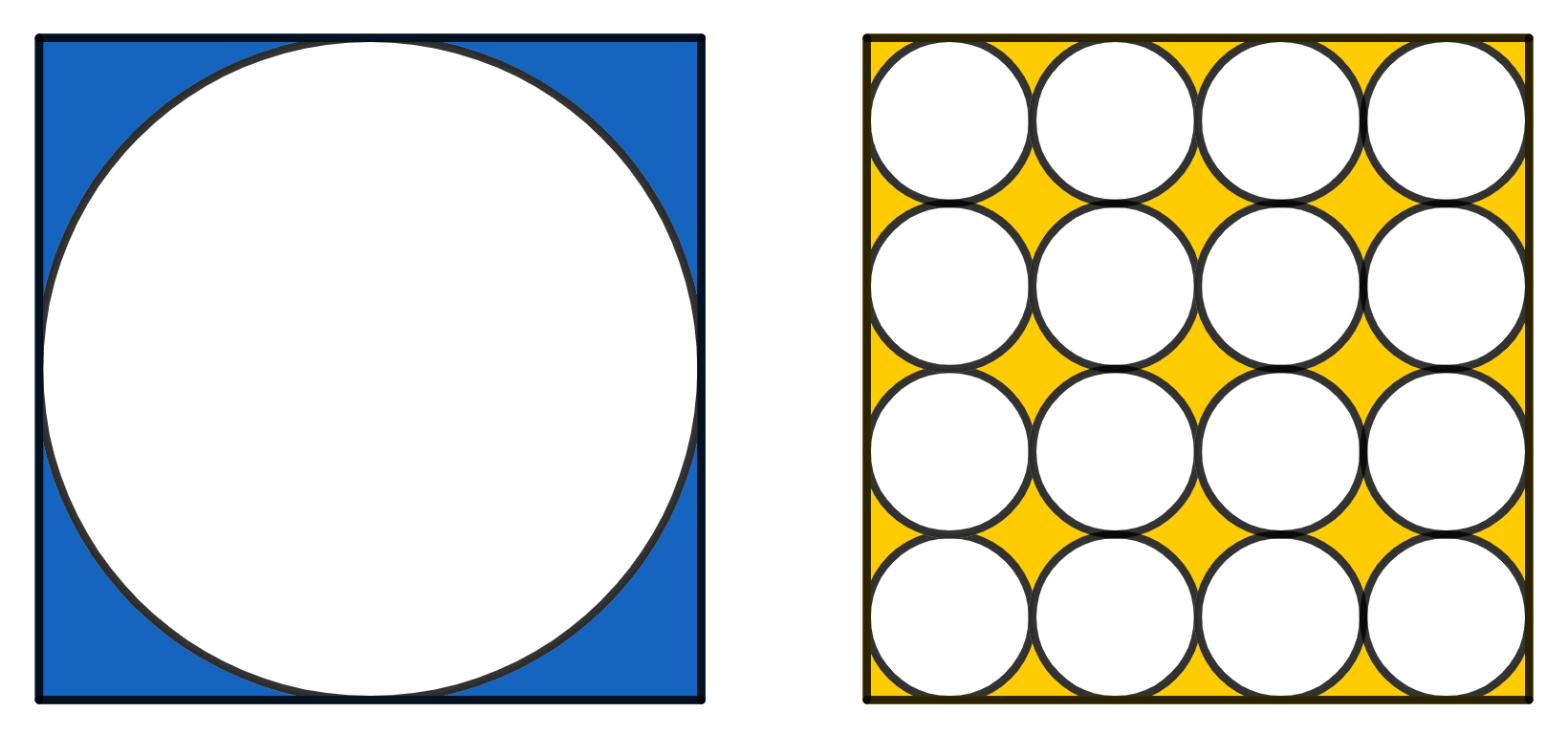
On the left there is a circle inscribed in a square of side 1. On the right there are 16 smaller, identical circles, which all together fit inside a square of side 1. Which area is greater, the yellow or the blue one?
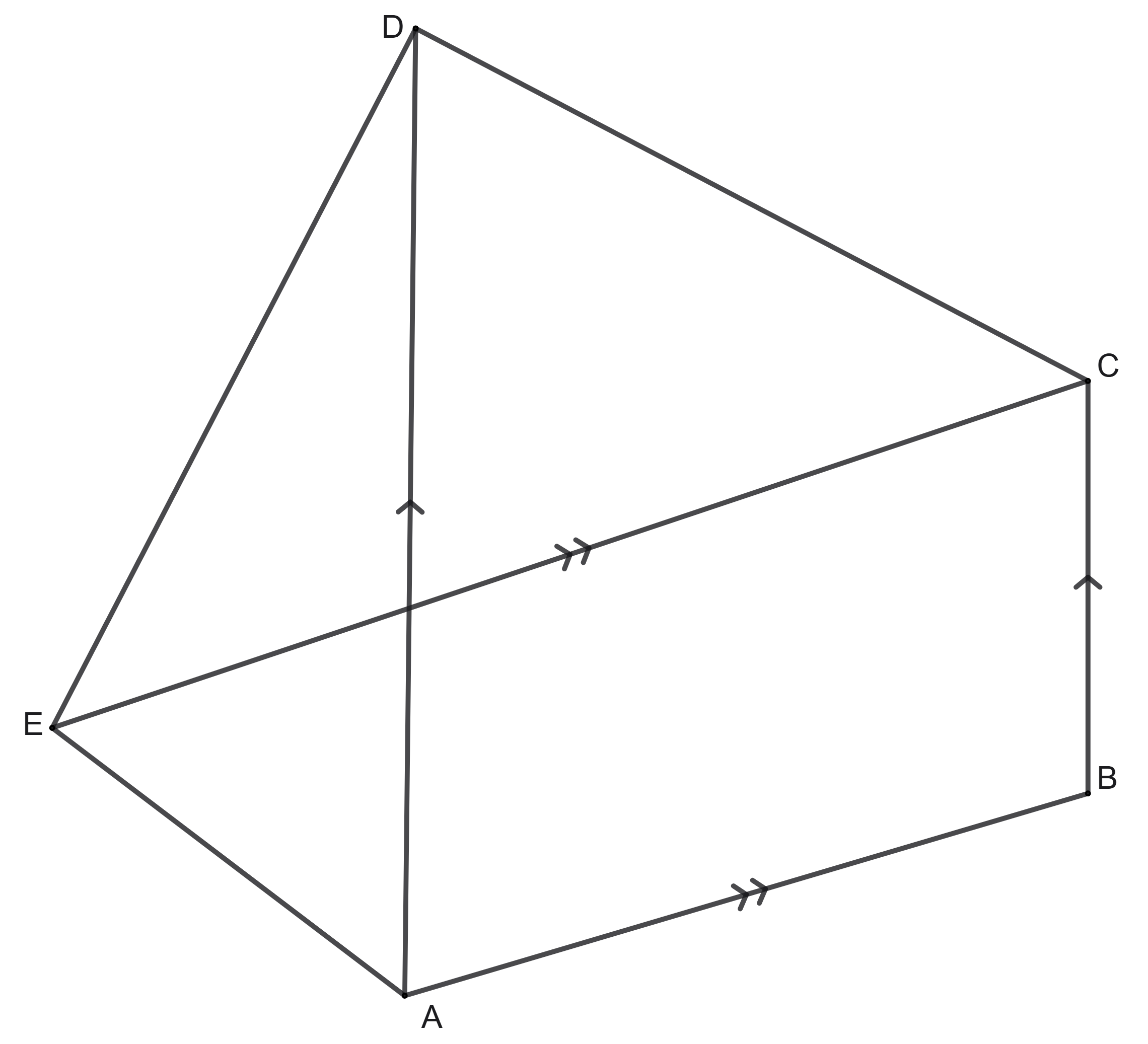
In a pentagon \(ABCDE\), diagonal \(AD\) is parallel to the side \(BC\) and the diagonal \(CE\) is parallel to the side \(AB\). Show that the areas of the triangles \(\triangle ABE\) and \(\triangle BCD\) are the same.
120 unit squares are placed inside a \(20 \times 25\) rectangle. Prove that it will always be possible to place a circle with diameter 1 inside the rectangle, without it overlapping with any of the unit squares.
You are given \(7\) straight lines on a plane, no two of which are parallel. Prove that there will be two lines such that the angle between them is less than \(26^{\circ}\).
Two lines on the plane intersect at an angle \(\alpha\). On one of them there is a flea. Every second it jumps from one line to the other (the point of intersection is considered to belong to both straight lines). It is known that the length of each of her jumps is 1 and that she never returns to the place where she was a second ago. After some time, the flea returned to its original point. Prove that for the angle \(\alpha\) the value \(\alpha/\pi\) is a rational number.
On a circle of radius 1, the point \(O\) is marked and from this point, to the right, a notch is marked using a compass of radius \(l\). From the obtained notch \(O_1\), a new notch is marked, in the same direction with the same radius and this is process is repeated 1968 times. After this, the circle is cut at all 1968 notches, and we get 1968 arcs. How many different lengths of arcs can this result in?