Problems
After having lots of practice with cutting different hexagons with a single cut Jennifer thinks she found a special one. She found a hexagon which cannot be cut into two quadrilaterals. Provide an example of such a hexagon.
Two people had two square cakes. Each person made 2 straight cuts from edge to edge on their cake. After doing this, one person ended up with three pieces, and the other with four. How could this be?
How can you divide a pancake with three straight sections into 4, 5, 6, 7 parts?
What is the maximum number of pieces that a round pancake can be divided into with three straight cuts?
In Neverland, there are magic laws of nature, one of which reads: “A magic carpet will fly only when it has a rectangular shape.” Frosty the Snowman had a magic carpet measuring \(9 \times 12\). One day, the Grinch crept up and cut off a small rug of size \(1 \times 8\) from this carpet. Frosty was very upset and wanted to cut off another \(1 \times 4\) piece to make a rectangle of \(8 \times 12\), but the Wise Owl suggested that he act differently. Instead he cut the carpet into three parts, of which a square magic carpet with a size of \(10 \times 10\) could be sown with magic threads. Can you guess how the Wise Owl restructured the ruined carpet?
During the ball every young man danced the waltz with a girl, who was either more beautiful than the one he danced with during the previous dance, or more intelligent, but most of the men (at least 80%) – with a girl who was at the same time more beautiful and more intelligent. Could this happen? (There was an equal number of boys and girls at the ball.)
On a plane there is a square, and invisible ink is dotted at a point \(P\). A person with special glasses can see the spot. If we draw a straight line, then the person will answer the question of on which side of the line does \(P\) lie (if \(P\) lies on the line, then he says that \(P\) lies on the line).
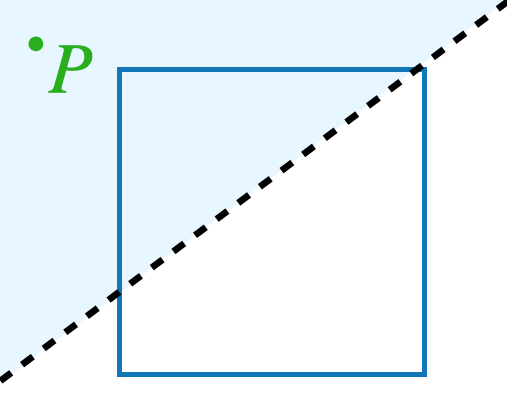
What is the smallest number of such questions you need to ask to find out if the point \(P\) is inside the square?
Due to a mistake in the bakery, a cake that was supposed to be shaped as two concentric pieces (like on the right diagram below) came out like the left diagram below. Find the smallest number of pieces the cake should be cut into in order to rearrange the pieces into the cake on the right side of the picture.
Note that the cake is \(\textit{not}\) tiered like a wedding cake, but is shaped like a cylinder with a flat top. Curved cuts are allowed.
One cell was cut out of a \(3\times6\) rectangle, as seen in the diagram. How should you glue this cell in a different place to get a figure that can be cut into two identical ones? If needed, the resulting parts can be rotated and reflected.
A piece containing exactly \(4\) black cells is cut out from a regular \(8\) by \(8\) chessboard. You are only allowed to cut along the edges of the cells and the piece must be connected - namely you cannot have cells attached only with a vertex, they have to share a common edge.
Find the largest possible area of such a piece.