Problems

At the cat show, 10 male cats and 19 female cats sit in a row where next to each female cat sits a fatter male cat. Prove that next to each male cat is a female cat, which is thinner than it.

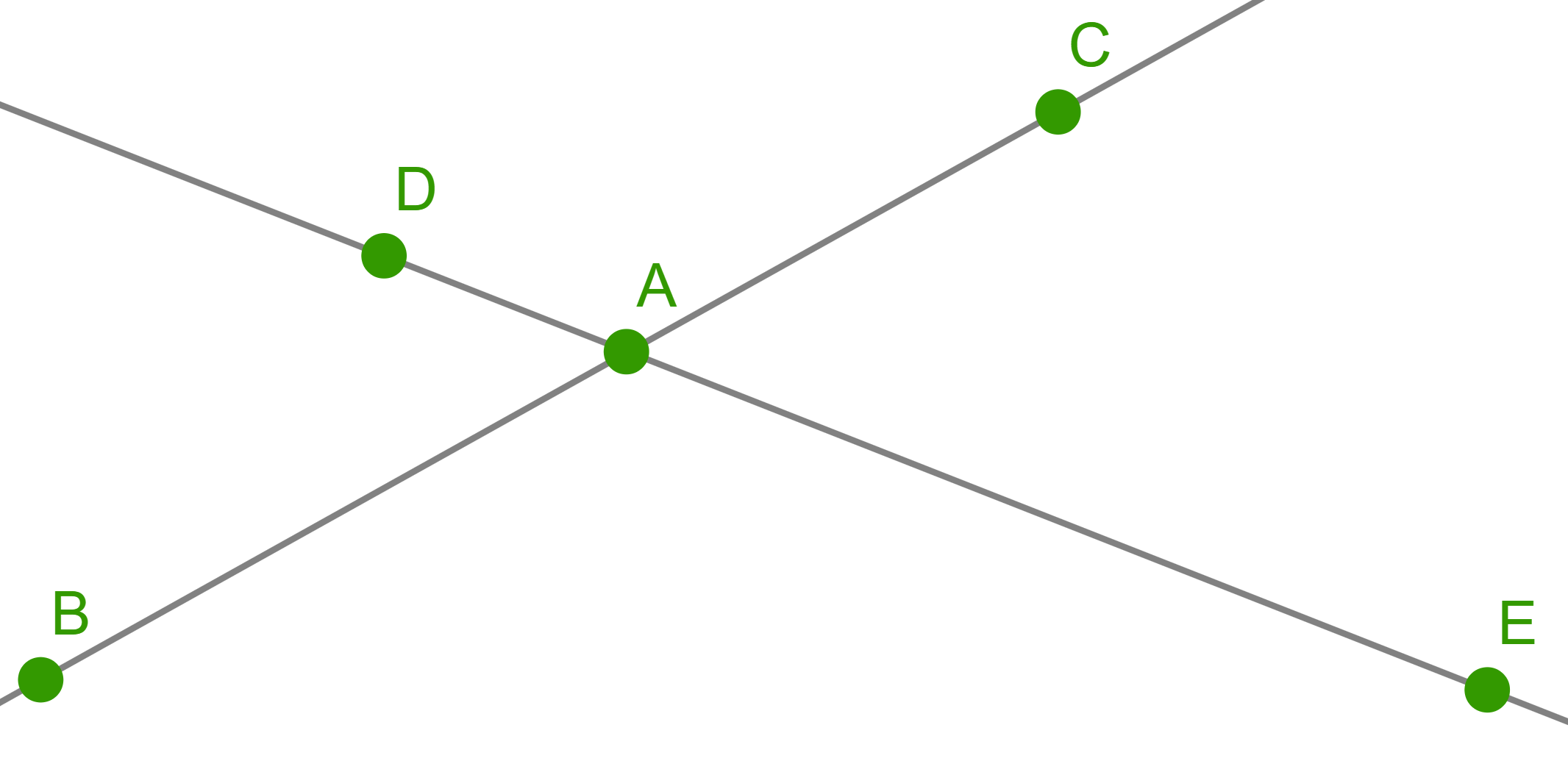
Five oaks are planted along two linear park alleys in such a way that there are three oaks along each alley, see picture. Where should we plant the sixth oak so that it will be possible to lay two more linear alleys, along each of which there would also be three oak trees growing?

Decipher the following puzzle. All the numbers indicated by the letter E, are even (not necessarily equal); all the numbers indicated by the letter O are odd (also not necessarily equal).

The smell of a flowering lavender plant diffuses through a radius of 20 m around it. How many lavender plants must be planted along a straight 400m path so that the smell of the lavender reaches every point on the path.

In a vase, there is a bouquet of 7 white and blue lilac branches. It is known that 1) at least one branch is white, 2) out of any two branches, at least one is blue. How many white branches and how many blue are there in the bouquet?

Prove that for every natural number \(n > 1\) the equality: \[\lfloor n^{1 / 2}\rfloor + \lfloor n^{1/ 3}\rfloor + \dots + \lfloor n^{1 / n}\rfloor = \lfloor \log_{2}n\rfloor + \lfloor \log_{3}n\rfloor + \dots + \lfloor \log_{n}n\rfloor\] is satisfied.

Given an endless piece of chequered paper with a cell side equal to one. The distance between two cells is the length of the shortest path parallel to cell lines from one cell to the other (it is considered the path of the center of a rook). What is the smallest number of colors to paint the board (each cell is painted with one color), so that two cells, located at a distance of 6, are always painted with different colors?

A group of numbers \(A_1, A_2, \dots , A_{100}\) is created by somehow re-arranging the numbers \(1, 2, \dots , 100\).

100 numbers are created as follows: \[B_1=A_1,\ B_2=A_1+A_2,\ B_3=A_1+A_2+A_3,\ \dots ,\ B_{100} = A_1+A_2+A_3\dots +A_{100}.\]

Prove that there will always be at least 11 different remainders when dividing the numbers \(B_1, B_2, \dots , B_{100}\) by 100.

Prove that in any group of 7 natural numbers – not necessarily consecutive – it is possible to choose three numbers such that their sum is divisible by 3.

a) We are given two cogs, each with 14 teeth. They are placed on top of one another, so that their teeth are in line with one another and their projection looks like a single cog. After this 4 teeth are removed from each cog, the same 4 teeth on each one. Is it always then possible to rotate one of the cogs with respect to the other so that the projection of the two partially toothless cogs appears as a single complete cog? The cogs can be rotated in the same plane, but cannot be flipped over.

b) The same question, but this time two cogs of 13 teeth each from which 4 are again removed?