Problems
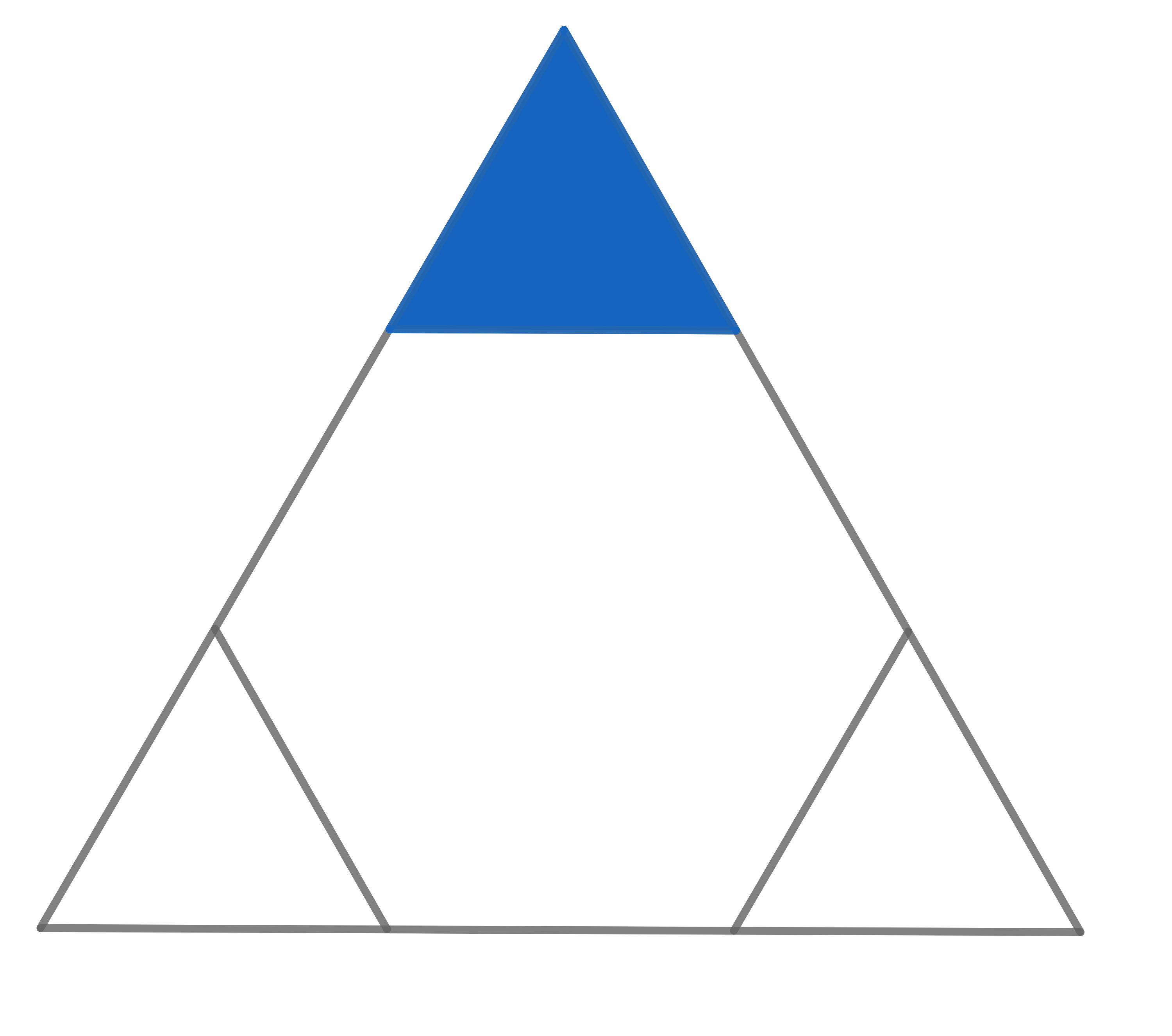
The triangle visible in the picture is equilateral. The hexagon inside is a regular hexagon. If the area of the whole big triangle is \(18\), find the area of the small blue triangle.
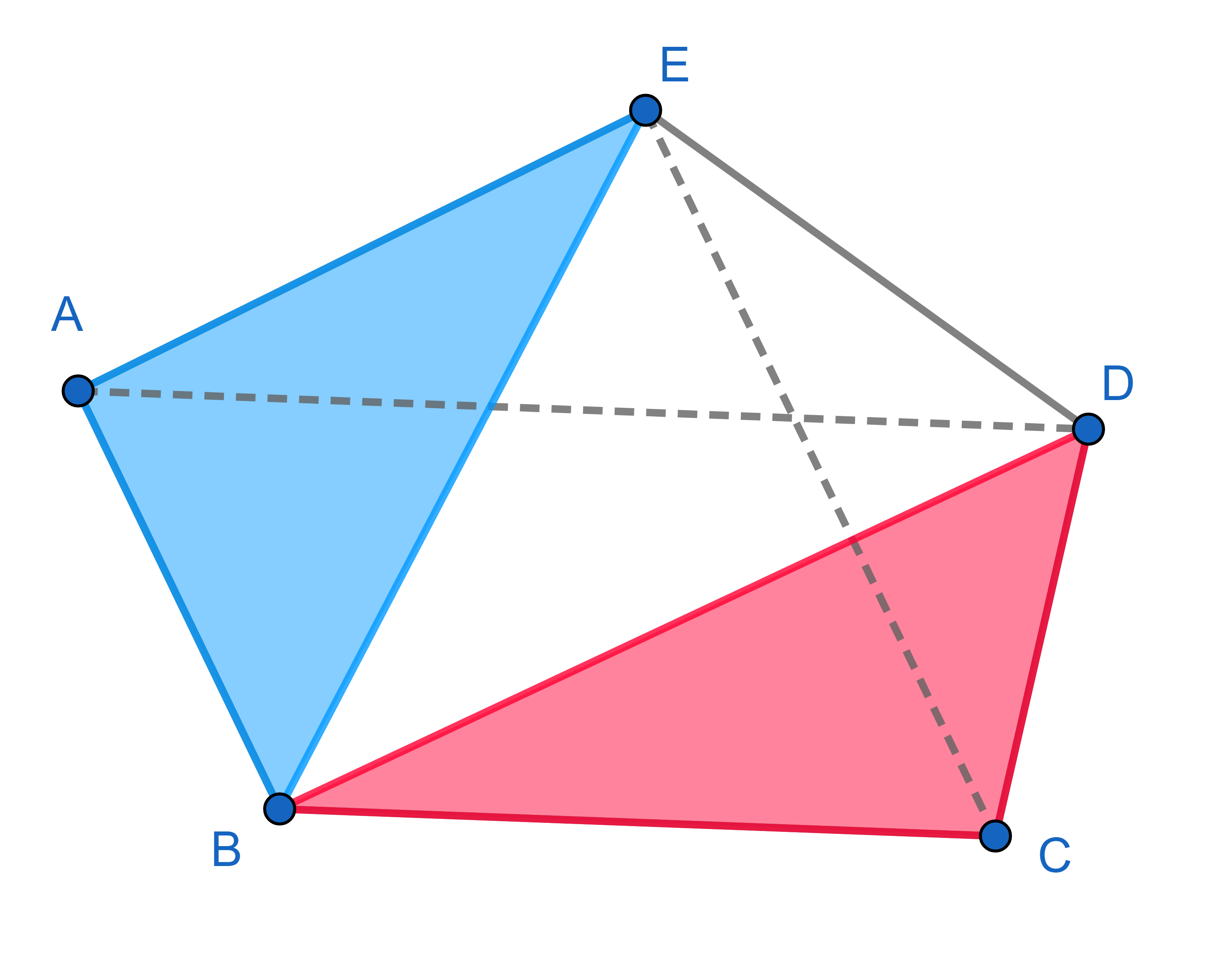
In a pentagon \(ABCDE\), diagonal \(AD\) is parallel to the side \(BC\) and the diagonal \(CE\) is parallel to the side \(AB\). Show that the areas of the triangles \(\triangle ABE\) and \(\triangle BCD\) are the same.
Which triangle has the largest area? The dots form a regular grid.
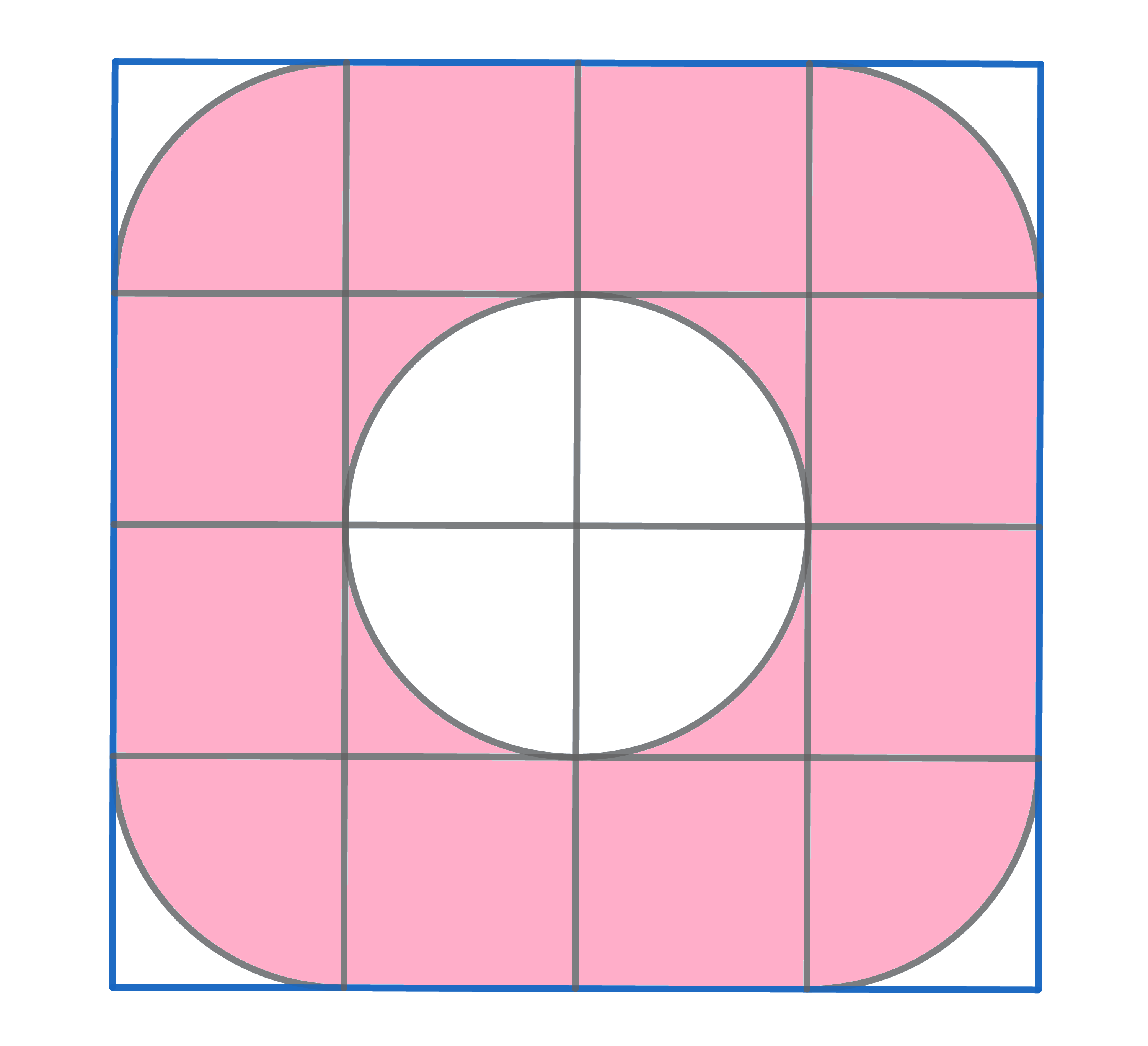
What is the ratio between the red and blue area? All shapes are semicircles and the red ones have equal radii.

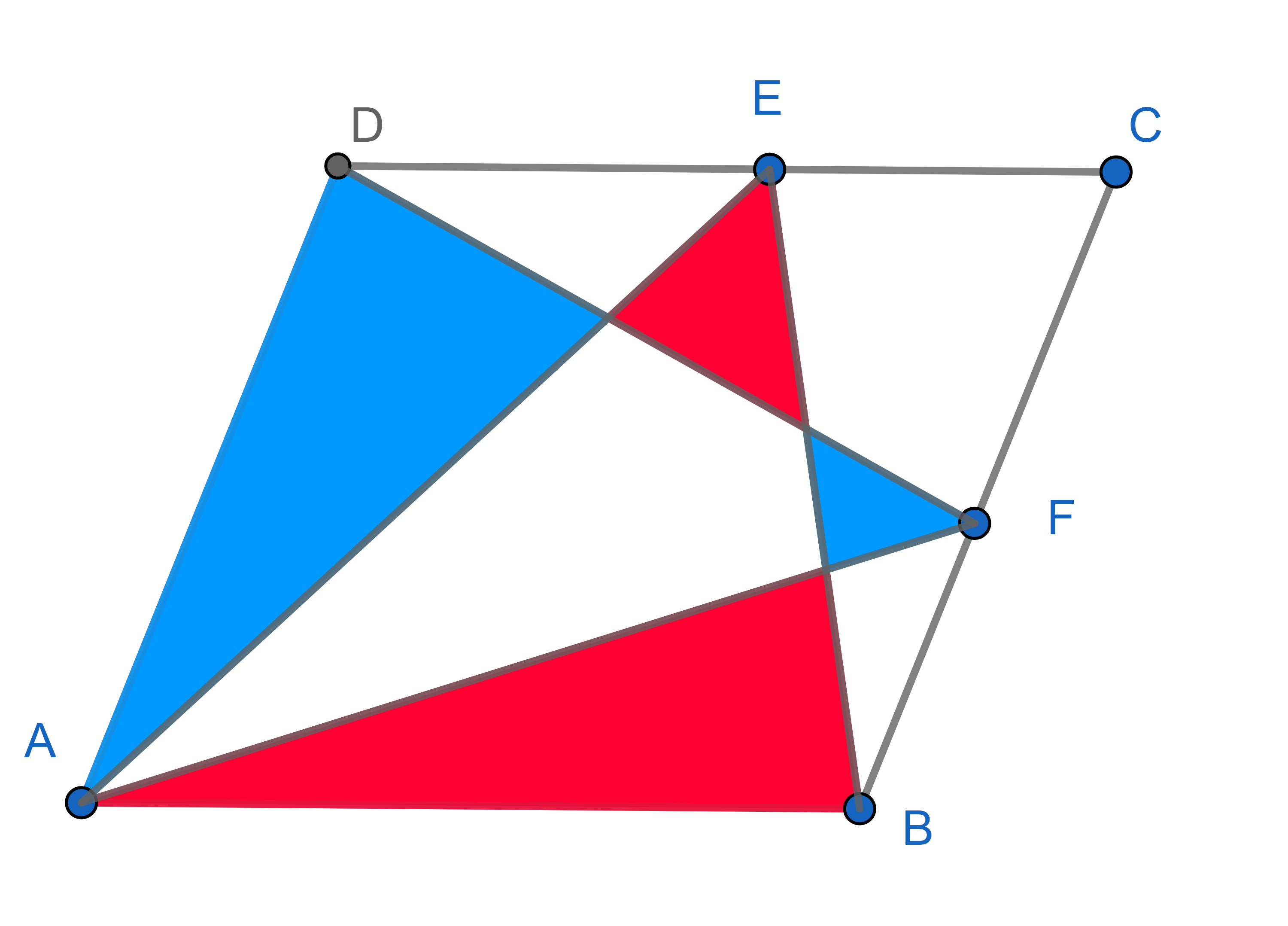
In a parallelogram \(ABCD\), point \(E\) belongs to the side \(CD\) and point \(F\) belongs to the side \(BC\). Show that the total red area is the same as the total blue area:
The figure below is a regular pentagram. What is larger, the black area or the blue area?

Suppose you only knew the area formula of a triangle for right-angled triangles. That is, if a base with length \(b\) and a height \(h\) of a triangle meet at a right angle, you know that the area of the triangle is \(\frac{1}{2}bh\). Can you prove the usual area formula for a general triangle?
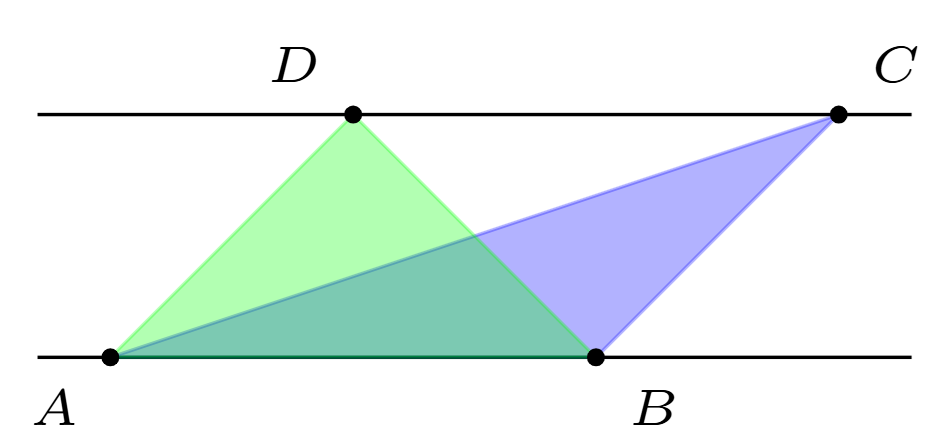
There is a pair of parallel lines. The point \(A\) and \(B\) lie on one of the lines. The point \(C\) and \(D\) lies on the other line. We can form triangles \(\triangle ABC\) and \(\triangle ABD\). Prove that the areas of triangles \(\triangle ABC\) and \(\triangle ABD\) are equal.
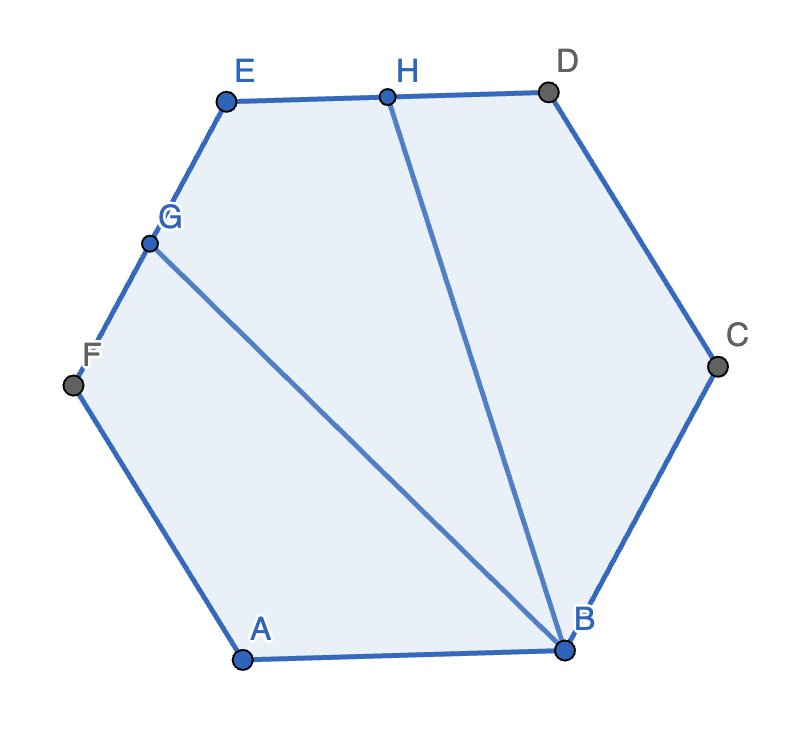
Let \(ABCDEF\) be a regular hexagon. Points \(G\) and \(H\) lie on \(EF\) and \(DE\) respectively such that \(|EG|=|EH|\). Furthermore, the area of quadrilateral \(ABGF\) is equal to the area of quadrilateral \(BGEH\), which are both equal to the area of \(BCDH\). What’s the ratio \(\frac{|EG|}{|EF|}\)?