Problems
James furiously cuts a rectangular sheet of paper with scissors. Every second he cuts a random piece by an unsystematic rectilinear cut into two parts.
a) Find the mathematical expectation of the number of sides of a polygon (made from a piece of paper) that James randomly picks up after an hour of such work.
b) Solve the same problem if at first the piece of paper had the form of an arbitrary polygon.
The upper side of a piece of square paper is white, and the lower one is red. In the square, a point F is randomly chosen. Then the square is bent so that one randomly selected vertex overlaps the point F. Find the mathematical expectation of the number of sides of the red polygon that appears.
A regular dice is thrown many times. Find the mathematical expectation of the number of rolls made before the moment when the sum of all rolled points reaches 2010 (that is, it became no less than 2010).
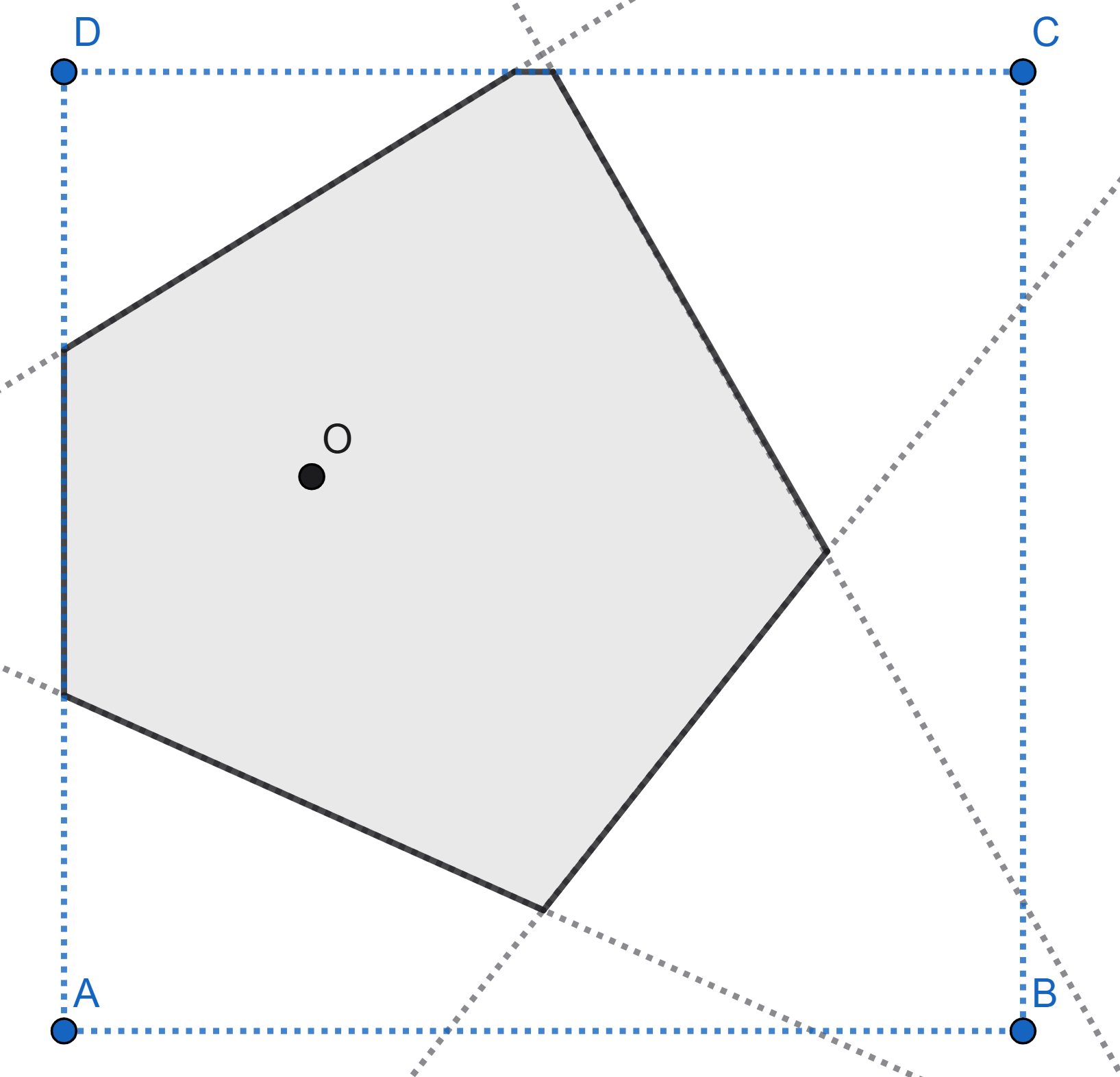
The point \(O\) is randomly chosen on piece of square paper. Then the square is folded in such a way that each vertex is overlaid on the point \(O\). The figure shows one of the possible folding schemes. Find the mathematical expectation of the number of sides of the polygon that appears.
A fair dice is thrown many times. It is known that at some point the total amount of points became equal to exactly 2010.
Find the mathematical expectation of the number of throws made to this point.
The Scattered Scientist constructed a device consisting of a sensor and a transmitter. The average life expectancy of the sensor part is 3 years, the average lifetime of the transmitter is 5 years. Knowing the distribution of the lifetime of the sensor and the transmitter, the Scattered Scientist calculated that the average lifetime of the entire device is 3 years 8 months. Was the Scattered Scientist wrong in his calculations?
In a numerical set of \(n\) numbers, one of the numbers is 0 and another is 1.
a) What is the smallest possible variance of such a set of numbers?
b) What should be the set of numbers for this?
A fly moves from the origin only to the right or upwards along the lines of the integer grid (a monotonic wander). In each node of the net, the fly randomly selects the direction of further movement: upwards or to the right.
a) Prove that sooner or later the fly will reach the point with abscissa 2011.
b) Find the mathematical expectation of the ordinate of the fly at the moment when the fly reached the abscissa 2011.
The point \(O\), lying inside the triangle \(ABC\), is connected by segments with the vertices of the triangle. Prove that the variance of the set of angles \(AOB\), \(AOC\) and \(BOC\) is less than a) \(10\pi ^2/27\); b) \(2\pi ^2/9\).
At the sound of the whistle of the PE teacher, all 10 boys and 7 girls lined up randomly.
Find the mathematical expectation of the value “the number of girls standing to the left of all of the boys.”