Problems

A numeric set \(M\) containing 2003 distinct numbers is such that for every two distinct elements \(a, b\) in \(M\), the number \(a^2+ b\sqrt 2\) is rational. Prove that for any \(a\) in \(M\) the number \(q\sqrt 2\) is rational.

Solve the equation \((x + 1)^3 = x^3\).

Does there exist a function \(f (x)\) defined for all \(x \in \mathbb{R}\) and for all \(x, y \in \mathbb{R}\) satisfying the inequality \(| f (x + y) + \sin x + \sin y | < 2\)?

The functions \(f (x) - x\) and \(f (x^2) - x^6\) are defined for all positive \(x\) and increase. Prove that the function

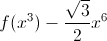
also increases for all positive \(x\).

The numbers \(p\) and \(q\) are such that the parabolas \(y = - 2x^2\) and \(y = x^2 + px + q\) intersect at two points, bounding a certain figure.

Find the equation of the vertical line dividing the area of this figure in half.

The quadratic trinomials \(f (x)\) and \(g (x)\) are such that \(f' (x) g' (x) \geq | f (x) | + | g (x) |\) for all real \(x\). Prove that the product \(f (x) g (x)\) is equal to the square of some trinomial.

Prove that if the numbers \(x, y, z\) satisfy the following system of equations for some values of \(p\) and \(q\): \[\begin{aligned} y &= x^2 + px + q,\\ z &= y^2 + py + q,\\ x &= z^2 + pz + q, \end{aligned}\] then the inequality \(x^2y + y^2z + z^2x \geq x^2z + y^2x + z^2y\) is satisfied.

Find \(x^3 +y^3\) if \(x+y=5\) and \(x+y+x^2 y +xy^2 =24\).

On the \(xy\)-plane shown below is the graph of the function \(y=ax^2 +c\). At which points does the graph of the function \(y=cx+a\) intersect the \(x\) and \(y\) axes?

Find the largest natural number \(n\) which satisfies \(n^{200} <5^{300}\).