Problems
Kai has a piece of ice in the shape of a “corner” (see the figure). The Snow Queen demanded that Kai cut it into four equal parts. How can he do this?

The surface of a \(3\times 3\times 3\) Rubik’s Cube contains \(54\) squares. What is the maximum number of squares we can mark so that no marked squares share at least one vertex?
Make sure you show that both (a) you can achieve this maximum and (b) that you can’t do better than this maximum.
A circle is covered with several arcs. These arcs can overlap one another, but none of them cover the entire circumference. Prove that it is always possible to select several of these arcs so that together they cover the entire circumference and add up to no more than \(720^{\circ}\).
A target consists of a triangle divided by three families of parallel lines into 100 equilateral unit triangles. A sniper shoots at the target. He aims at a particular equilateral triangle and either hits it or hits one of the adjacent triangles that share a side with the one he was aiming for. He can see the results of his shots and can choose when to stop shooting. What is the largest number of triangles that the sniper can guarantee he can hit exactly 5 times?
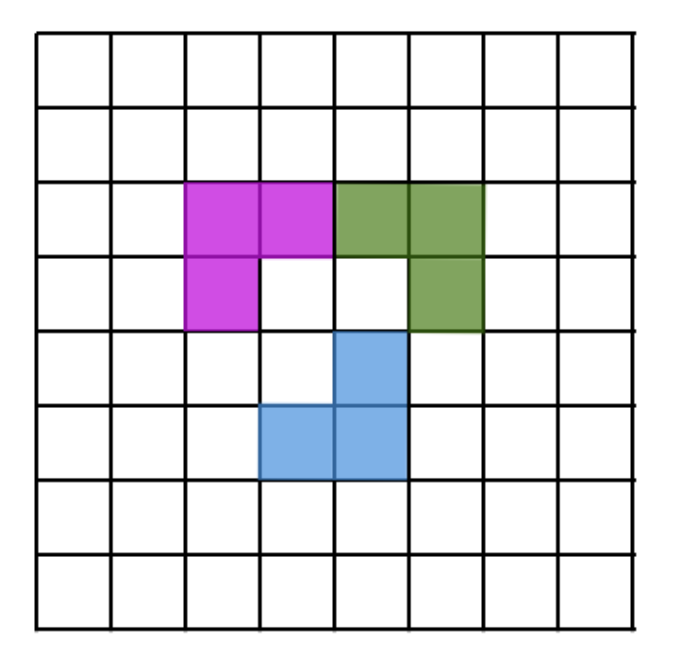
On an 8×8 grid (like a chessboard), an L-corner is a shape made of 3 little squares of the board that touch to make an L. You can turn the L any way you like. We place the L-corners so that none overlap. What is the fewest L-corners you must place so that no more L-corners can be added anywhere? Here is an example of how three L-corners may look like:
Is it possible to fill a \(5 \times 5\) board with \(1 \times 2\) dominoes?
One corner square was cut from a chessboard. What is the smallest number of equal triangles that can be cut into this shape?
Some open sectors – that is sectors of circles with infinite radii – completely cover a plane. Prove that the sum of the angles of these sectors is no less than \(360^\circ\).
10 magazines lie on a coffee table, completely covering it. Prove that you can remove five of them so that the remaining magazines will cover at least half of the table.
Prove that rational numbers from \([0; 1]\) can be covered by a system of intervals of total length no greater than \(1/1000\).